Exercice 1.
Soit le système de la figure, $F=F_m e^{ j \left( \omega t \right)}$
1. Etablir l’équation différentielle du mouvement.
2. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement.
3. Trouver la pulsation de résonance ${\omega }_r$.
4. Trouver la puissance moyenne fournie au système.
5. Déduire la puissance maximale fournie au système.
6. Déduire les pulsations de coupures pour les quelles $P=\frac{\overline{P_{\max }}}{2}$.
7. Déduire la bande passante (on suppose que $\lambda <<{\omega }_0$).
8. Trouver la puissance moyenne dissipée par frottement. Exercice 2
Soit le système de la figure, $F=F_m\cos \left(\omega t\right)$
1. Etablir l’équation différentielle du mouvement.
2. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement.
3. Trouver la pulsation de résonance ${\omega }_r$.
4. Trouver la puissance moyenne fournie au système.
5. Déduire la puissance maximale fournie au système.
6. Déduire les pulsations de coupures pour les quelles $P=\frac{\overline{P_{\max }}}{2}$.
7. Déduire la bande passante (on suppose que $\lambda <<{\omega }_0$).
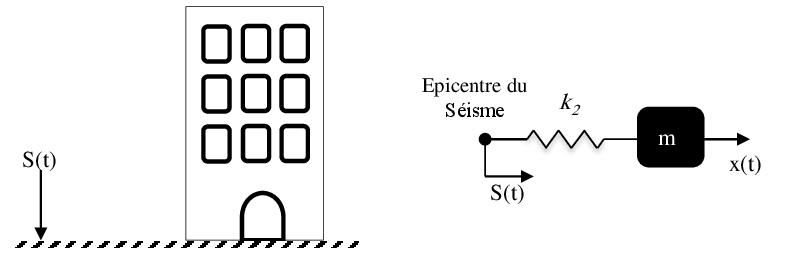
8. Trouver la puissance moyenne dissipée par frottement. Exercice 3
Soit un immeuble modélisé par le système physique représenté par une masse m et un ressort de raideur k subit à un mouvement sismique sinusoïdal d’amplitude a de forme $S\left(t\right)=a \cos (\omega t)$.
1. Établir l’équation différentielle du mouvement.
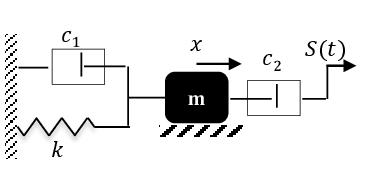
2. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement.Trouver la pulsation de résonance. Exercice 4
Soit le système de la figure. Un déplacement $S\left(t\right)=a \cos (\omega t)$est imposé sur l’extrémité droite du ressort.
1. Établir l’équation différentielle du mouvement.
2. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement. Trouver la pulsation de résonance. Exercice 5
Soit le système de la figure, $S=S_m\sin \left(\omega t\right)$.
1. Établir l’équation différentielle du mouvement.
2. Déterminer la pulsation propre ainsi que le facteur d’amortissement

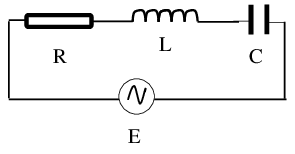
Exercice 6
Soit le circuit excité de la figure, $E\left(t\right)=E_m\cos \left(\omega t\right)$.
1. Trouver l’équation du mouvement de la charge électrique Q circulant dans le circuit.
2. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement. 3. Trouver la pulsation de résonance ${\omega }_r$.
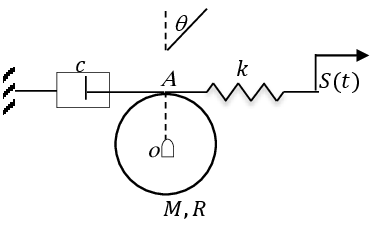
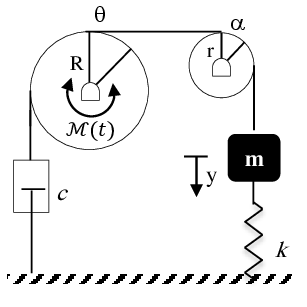
Exercice 7
Dans le système de la figure, les deux poulies sont de masses négligeables. Le système est met en oscillations par un moment de couple $M\left(t\right)=M_0\cos (\omega t)$ appliqué au disque de rayon R.
1. Déterminer le degré de liberté du système.
2. Établir l’équation différentielle du mouvement pour la coordonnée $\theta$.
3. Trouver en utilisant la notation complexe la solution permanente de l’équation différentielle du mouvement.
4. Trouver la pulsation de résonance ${\omega }_r$.
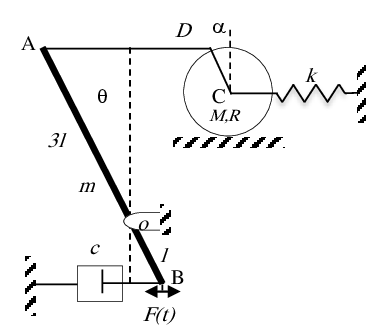
Exercice 8
Le système mécanique de la figure, est composé d’un disque homogène (M, R) roule sans glissement sur un plan horizontal, d’une barre AB (m, 4l) qui peut osciller autour d’un axe O perpendiculaire au plan du mouvement, d’un ressort k et d’un amortisseur c. La barre horizontale DA est de masse négligeable.
1. Etablir l’équation différentielle du mouvement pour la coordonnée $\theta$.
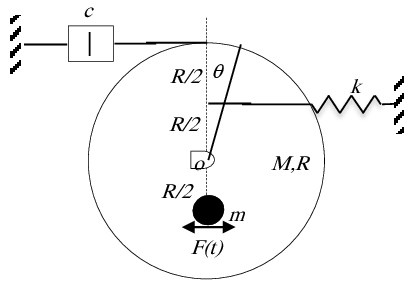
Exercice 9
Un système constitué d'un disque, homogène, de masse M et de rayon R, peut osciller sans frottement autour de son axe horizontal O. Ce disque est relié à un bâti par un ressort de raideur k, à une distance R/2 et d’un amortisseur de coefficient c. Une masse m est fixée au disque à une distance R/2 de O et fait un mouvement circulaire avec le mouvement du disque. Cette masse est soumise à une force $F\left(t\right)=F_m\cos \omega \hspace{0.17em}t$. En considérant les oscillations de faibles amplitudes.
1. Etablir l’équation différentielle du mouvement.
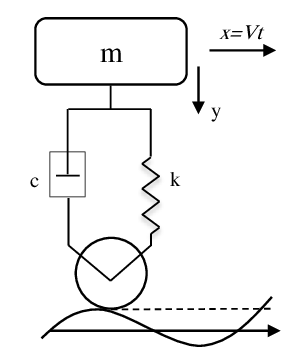
Exercice 10
La figure (a) représente une machine à laver constituée essentiellement d’une partie tournante (tambour) posée sur des supports anti vibrations représentés sur la figure par un ressort et un amortisseur. Le tambour a un rayon r et tourne avec une vitesse angulaire $\omega$. le tambour fait tourner le linge représenté par la masse m. Pour simplifier le problème on suppose que les mouvements de la machines à laver sont verticaux et représentés par la variable y. La masse de la machine est M.
1. Etablir l’équation différentielle du mouvement pour la coordonnée y.
2. Montrer qu’un tel dispositif est équivalent au schéma de la figure (b). Donner l’expression de la force équivalente F(t).
Exercice 11
La figure schématise une voiture de masse m dont le système suspension est représenté par un amortisseur de coefficient de frottement c et un ressort k. Les roues sont de masse négligeable devant m. Cette voiture se déplace dans la direction ox suivant une route ondulée dont le profil est supposé sinusoïdal : $y_1 \sin (2\pi x/\varsigma )$, à une vitesse V constante. La voiture se déplace suivant ox et sa position vertical est repérée par la variable y(t). on suppose qu’il n’y a pas de mouvement latéral (suivant l’axe oz).
1. Établir l’équation différentielle qui régit les variations de la coordonnée y au cours du temps. En déduire l’amplitude Y du mouvement.
Exercice 12
Soit le système forcé de la figure
1. Etablir l’équation différentielle du mouvement.








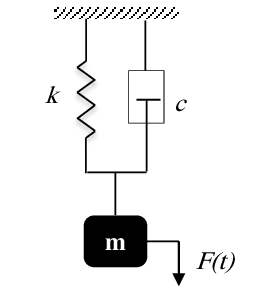
On impose au système de fonctionner en résonance à l’aide d’une force $F\left(t\right)=F_0 \cos \left(\omega t\right)$ .L’allure des oscillations en fonction du temps est donnée à la figure suivante :








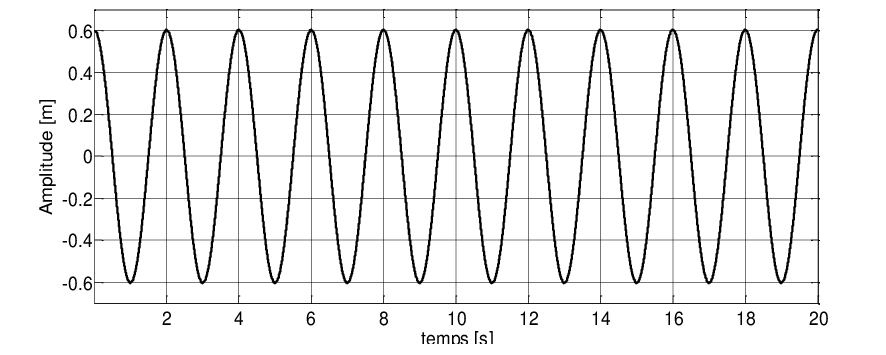
2. On donne : m=1 Kg ; F0 = 1 N.On cherche à identifier la suspension (c.à.d trouver les valeurs : k et c).
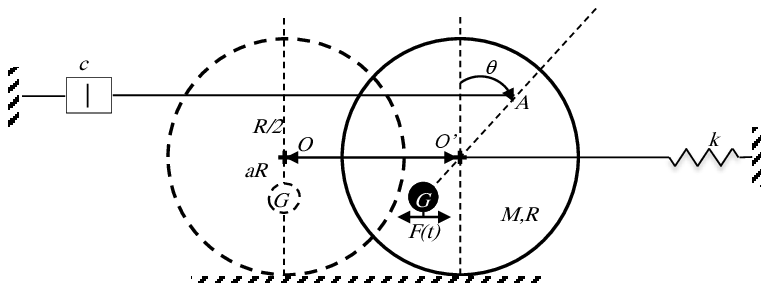
Exercice 13
Un système constitué d’un disque, homogène, de masse M et de rayon R, peut rouler sans glisser sur un plan horizontal. Ce disque est relié à un bâti par un ressort de raideur k, au point O et d’un amortisseur de coefficient c au point A tel que $\left|\overrightarrow{OA}\right|=\frac{R}{2}$. Une masse m=M/2 est fixée au disque au point G à une distance $\left|\overrightarrow{OG}\right|=a \times R$ tel que $0<a <1$. Cette masse est soumise à une force $F\left(t\right)=F\cos (\omega \hspace{0.17em}t)$. En considérant les cas des oscillations de faibles amplitudes :
1. Montrer que l’équation différentielle du mouvement du système est de la forme :
$\left[\left(6+2{(1-a)}^2\right)M\right] \ddot{\theta } + \left[\frac{4 k R+2M g a}{R}\right] \theta + \left[9 c\right] \dot{\theta } = \frac{4F\left(t\right)\left(1-a\right)}{R}$
2. On considère le cas d’un amortissement critique. Déterminer la valeur de k pour laquelle la puissance moyenne fournie au système est nulle.
On donne :
- M=500 Kg, R=1m.
- A l’instant t=0 :$\theta =0\hspace{0.17em}rd$ et V(0) =10 rd/s.
- A l’instant t=t1 : $\theta \left(t_1\right)={\theta }_{max}=0.5rd$ et V(t1)=0 rd/s. Exercice 14 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Soit le système de la figure
1. Déterminer les expressions de : la pulsation propre et du facteur d’amortissement.











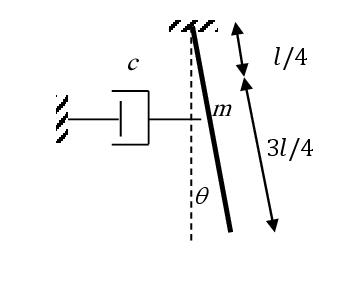
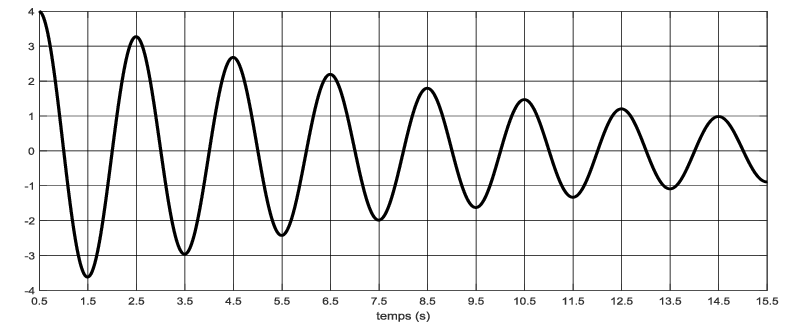
2. La figure suivante, représente l’allure du déplacement angulaire de la tige. Calculer la longueur l de la tige.











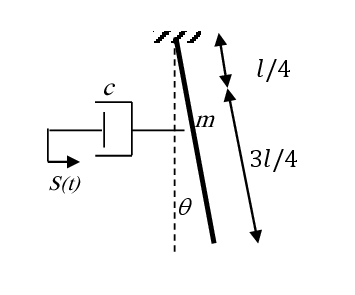
Un déplacement $S\left(t\right)=S_m \sin \left(\omega t\right)$ est imposé sur l’extrémité libre de l’amortisseur (Voir figure suivante).
3. Établir l’équation différentielle du mouvement .
4. Déterminer l’expression de la fonction d’excitation.












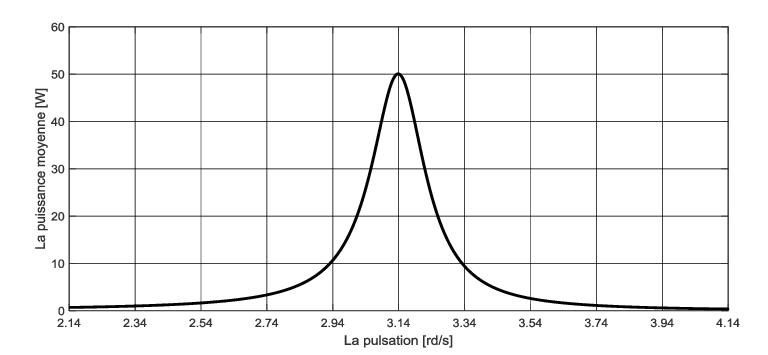
5. La figure suivante, représente l’allure de la puissance moyenne fournie au système en fonction de la pulsation $\omega$. Calculer la masse de la tige.











Exercice 15 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Soit le système forcé de la figure, on impose au système de fonctionner en résonance à l’aide d’une force $F\left(t\right)=F_m\cos (\omega \hspace{0.17em}t)$ .











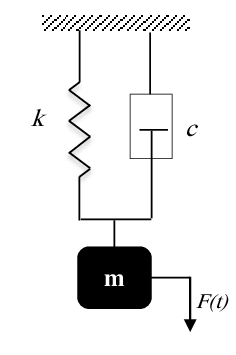
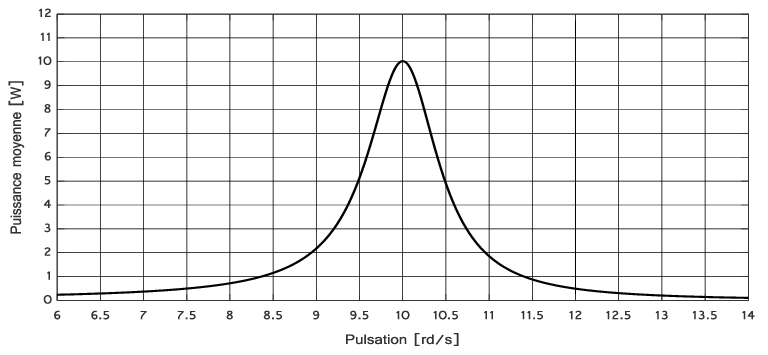
L’allure de la puissance moyenne fournie au système en fonction de la pulsation est donnée à la figure.
On donne : m= 5 Kg ;$F_m=10N$.
On cherche à identifier la suspension (c.à.d trouver les valeurs : k et c).
- En utilisant le graph, calculer k et c.











Exercice 16 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
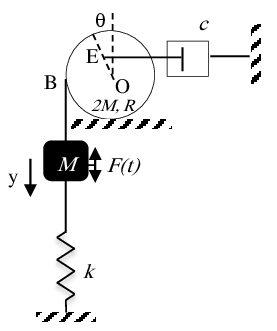
Soit le système mécanique composé d’un disque homogène ($2M, R$) qui peut rouler sans glisser sur un plan orizental, d’une masse ponctuelle $M$, d’un ressort $k$ et d’un amortisseur $c$ tel que $OE=R/2$ .
On donne : $F\left(t\right)=F_m\cos (\omega \hspace{0.17em}t)$.
Les mouvement sont de faibles oscillations d’où : $\sin \theta =\theta \text{ et }\cos \theta =\left(1-\frac{{\theta }^2}{2}\right)$.











1. Trouver une relation entre $\theta$ et y.
2. Calculer l’énergie cinétique
3. Calculer l’énergie potentielle.
4. Calculer la fonction de dissipation
5. Etablir l’équation différentielle du mouvement.
Exercice 17 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
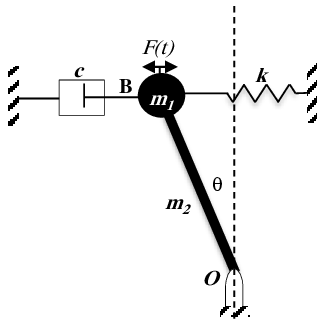
Soit le système mécanique composé d’une tige homogène ($m_2$) qui peut osciller autour de son centre de rotation o, d’une masse ponctuelle ($m_1$) fixée a la deuxième extrémité de la tige, d’un ressort k et d’un amortisseur c.
On donne : $F\left(t\right)=F_m\cos (\omega \hspace{0.17em}t), m=m_1=2\hspace{0.17em}{m}_2, OB=2\hspace{0.17em}L$.











1. Etablir l’équation différentielle du mouvement en fonction de : m, c, L, F et k.
2. Déduire la pulsation propre du système.
3. Trouver la solution permanente de l’équation différentielle du mouvement.
Exercice 18 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Soit le système mécanique composé d’une barre AB homogène (M, 2L) qui peut osciller autour de son centre de rotation, d’une barre BC de masse négligeable, d’un ressort k et d’un amortisseur c.
On donne : $F\left(t\right)=F_{m}cos(\omega \hspace{0.17em}t)$.











1. Déterminer le degré de liberté du système.
2. Calculer l’énergie cinétique du système.
3. Calculer l’énergie potentielle du système.
4. Calculer l’énergie de dissipation du système.
5. Etablir l’équation différentielle du mouvement pour la coordonnée $\theta$.
6. Déterminer l’amplitude des oscillations.
7. Déterminer la pulsation de résonance.
8. Déterminer l’amplitude des oscillations en présence de résonance.
Exercice 19 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Soit le système de la figure











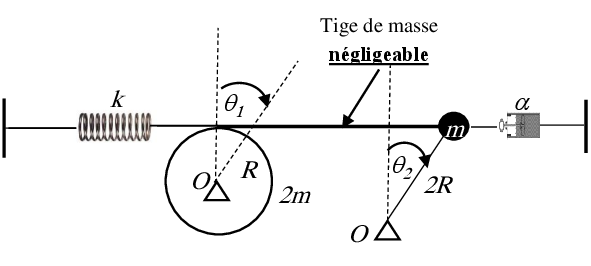
Pour des petites oscillations $\sin \theta =\theta \text{ et }\cos \theta =\left(1-\frac{{\theta }^2}{2}\right)$ :
1. Montrer que le système est à 01 DDL.
2. Déduire le Lagrangien du système ainsi que la pulsation propre.
3. On applique une force $F\left(t\right)=F_0\hspace{0.17em}{e}^{(j\omega \hspace{0.17em}t)}$ au point A. Trouver l’équation différentielle du mouvement.
4. Sachant que la solution particulière de l’équation du mouvement est de la forme ${\theta }_p\left(t\right)=A\hspace{0.17em}{e}^{(\omega t-\delta )}$, Déterminer l’amplitude et la phase.
5. Calculer la bonde passante et le facteur de qualité.
Exercice 20 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Soit le système de la figure











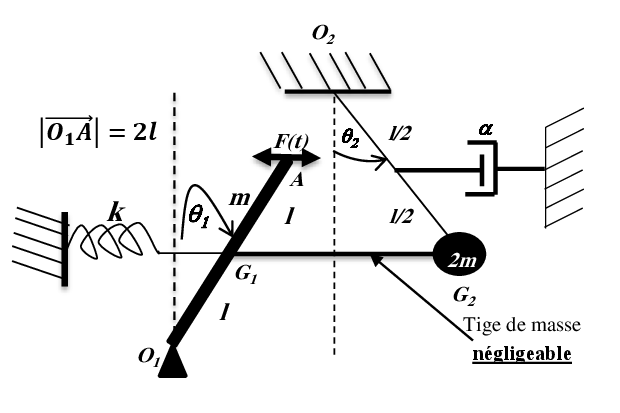
Pour des petites oscillations : $\sin \theta =\theta \text{ et }\cos \theta =\left(1-\frac{{\theta }^2}{2}\right)$ :
1. Calculer le degré de liberté du système.
2. Montrer que le Lagrangien du système est égale à : $L=\frac{1}{2}(\frac{10 }{3}m l^2){{\dot{\theta }}_1}^2-\frac{1}{2}(k l^2\text{+ }m gl){{\theta }_1}^2+cst$
3. On applique une force $F\left(t\right)=F_0\hspace{0.17em}{e}^{(j\omega \hspace{0.17em}t)}$ au point A. Trouver l’équation différentielle du mouvement.
4. Déduire la pulsation propre ainsi que le facteur d’amortissement du système.
5. Sachant que la solution particulière de l’équation du mouvement est de la forme : ${\theta }_p\left(t\right)=A e^{j(\omega t-\delta )}$, Déterminer l’amplitude et la phase.
6. Déterminer la bonde passante et le facteur de qualité.
Exercice 21 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Soit le système de la figure











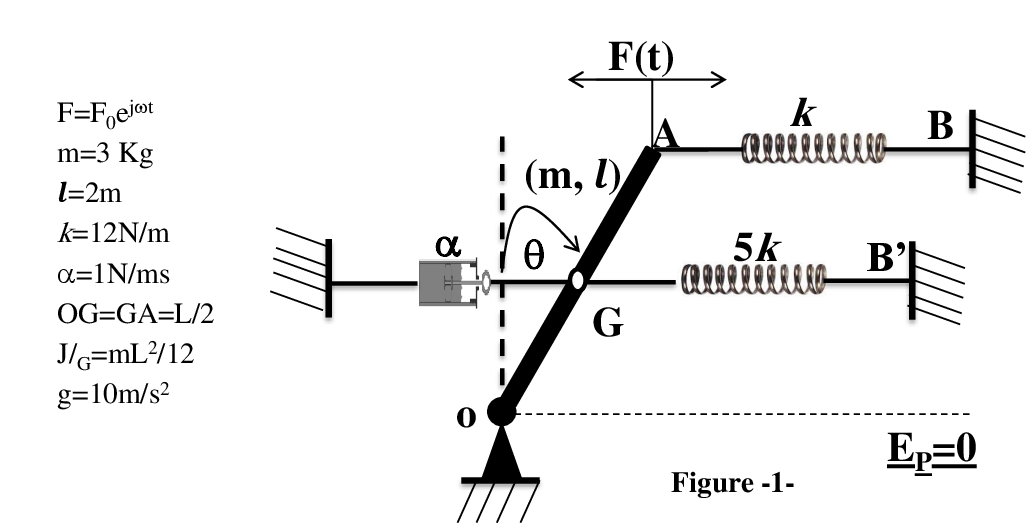
1. Déterminer le lagrangien du système, sachant que le système effectue des oscillations de faibles amplitudes : $\sin \theta =\theta \text{ et }\cos \theta =\left(1-{}^{{\theta }^2}/_2\right)$
2. Le point A est soumis à une force $F\left(t\right)=F_0\hspace{0.17em}{e}^{(j\omega \hspace{0.17em}t)}$. Etablir l’équation du mouvement et déduire la pulsation propre et le facteur d’amortissement.
3. En comparant entre la valeur de la pulsation propre et la valeur du facteur d’amortissement, déduire le type d’amortissement.
4. Pour ce type d’amortissement, et pour les conditions initiales suivantes : $\theta \left(0\right)=0,\hspace{0.17em}\hspace{0.17em}\dot{\theta }\left(0\right)={\dot{\theta }}_0$, déterminer la solution homogène $\theta_h$. Déterminer l’amplitude, la pulsation et la phase.
5. Sachant que la solution particulière de l’équation du mouvement est de la forme ${\theta }_p\left(t\right)=A\cos (\omega t-\delta )$, déterminer l’amplitude et la phase.
6. Calculer la bonde passante et le facteur de qualité.
Exercice 22 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
ne barre uniforme de masse m pouvant pivoter autour du point O, est connecté a ses extrémités par deux ressorts de constante de raideur k. I'extrémité P du ressort "PQ" est soumise à un déplacement sinusoidale $x\left(t\right)=x_0 \sin \omega \hspace{0.17em}t$ comme le montrent les figures suivantes :.











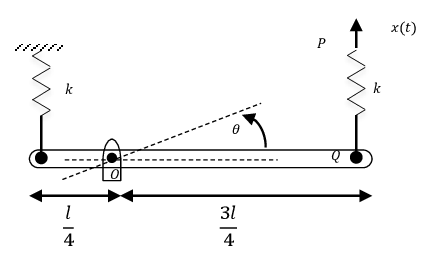
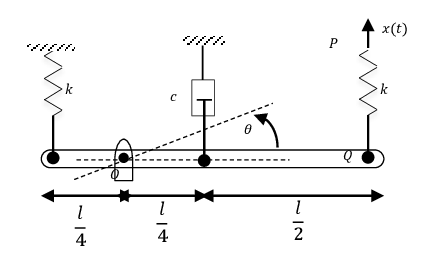
Trouver pour les deux figures le déplacement angulaire en régime permanent de la barre quand :
l = 1 m, k = 1000 N/m, m = 10\: kg, x0 = 1 cm, $\omega \hspace{0.17em}=10\hspace{0.17em}rd/s$ et c=500\: Ns/m,
Exercice 23 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Le dispositif mécanique de la figure est un instrument sismique qui consiste en une masse (m), un ressort (k), un amortisseur (c) et un traceur qui donne le mouvement de la masse m en fonction du temps.
Soit x(t) le mouvement de la masse m et y(t) le mouvement de la base que l'on suppose de la forme $y\left(t\right)=Y\hspace{0.17em}\sin \omega \hspace{0.17em}t$.











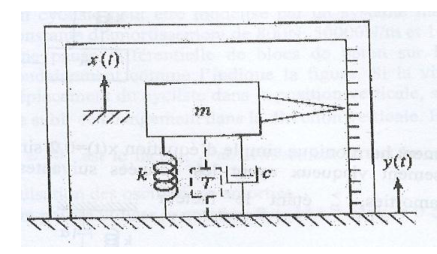
1. Établir, l'équation du mouvement de la masse $m$ en fonction du déplacement relatif z(t)=x(t)-y(t).
2. Déterminer la solution stationnaire z(t). Cette solution est donnée dans la forme $z\left(t\right)=Z\hspace{0.17em}\sin (\omega \hspace{0.17em}t-\delta )$.
La variation [Z/Y] en fonction du rapport des fréquence $r = \frac{{\displaystyle \omega }}{{\displaystyle {\omega }_0}}$ est donnée dans la figure.











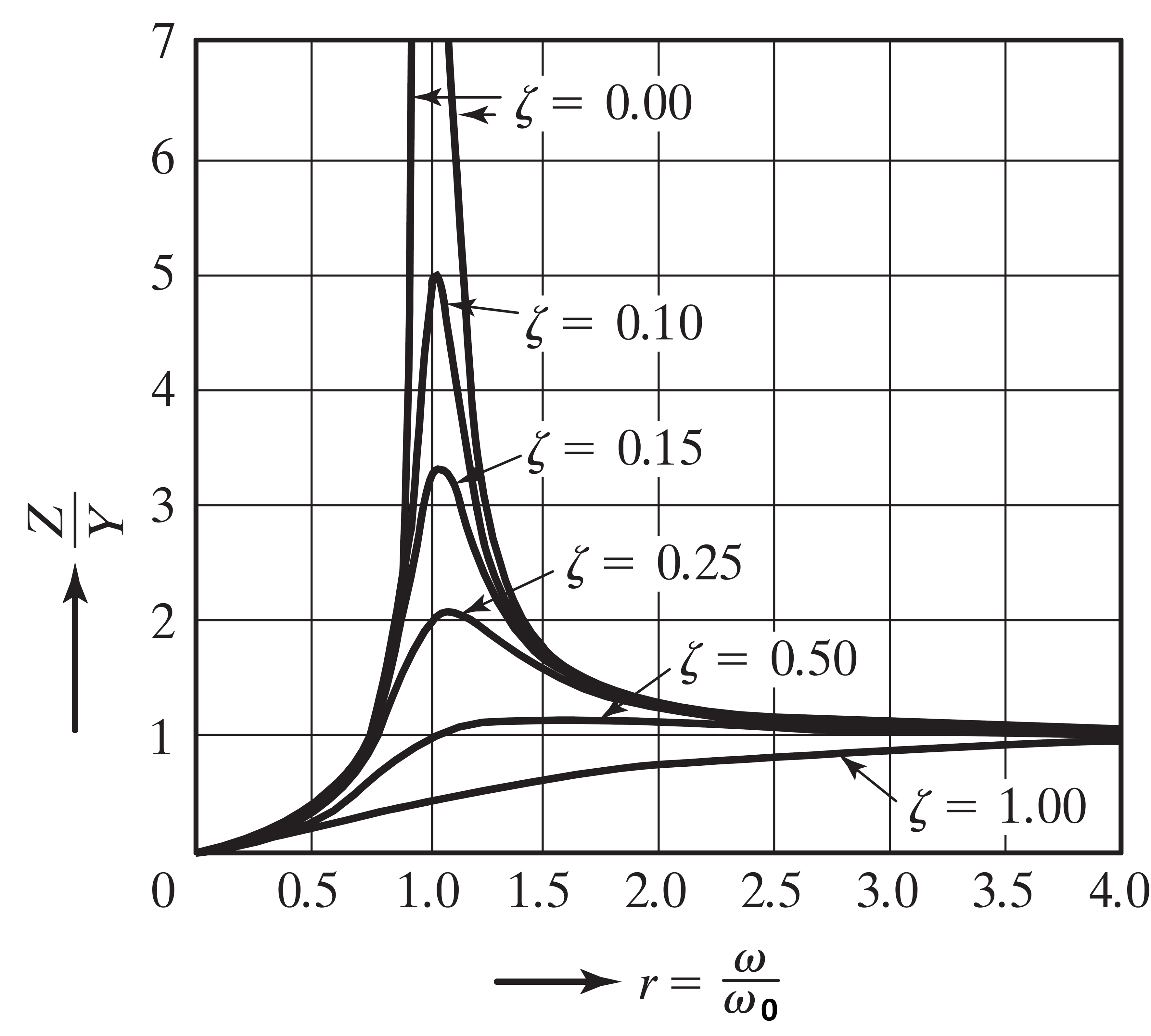
3. Dans le cas d'un ressort de faible raideur, la pulsation propres ${\omega }_0$ est petite devant la pulsation $\omega$. Écrire dans ce cas z(t), montrer que l'on peut ainsi déterminer l'amplitude Y des vibrations. Ceci est le principe du vibromètre.
4. Dans le cas d'un ressort de raideur élevé, ${\omega }_0$ est grande devant $\omega$, montrer que l'on peut déterminer ainsi l'accélération des vibrations ${\omega }^2\hspace{0.17em}Y$. Ceci est le principe de l'accéléromètre. Dites pour quoi les accéléromètres sont préférés aux vibrations.
Exercice 24 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un compresseur à air monocylindre de masse 100 kg est monté sur des supports en caoutchouc comme le montre la figure, les constantes d'élasticité et d'amortissement des supports en caoutchouc sont données par : $k={10}^6\hspace{0.17em}N/m$ et c =2000 Ns/m, respectivement.











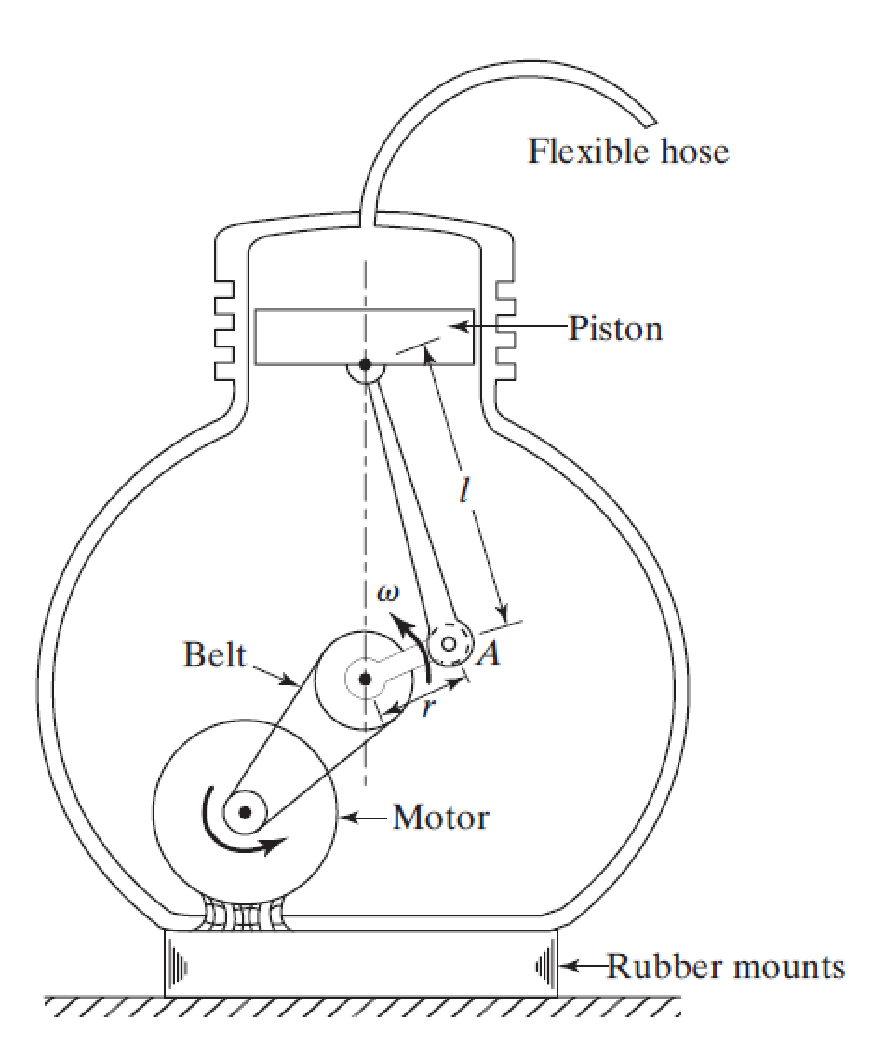
Si le déséquilibre de rotation du compresseur est équivalent à une masse de 0,1 kg localisée à la fin de l'essieu (point A), déterminer la réponse du compresseur à une vitesse de l'essieu de 3000 rpm. Supposer r=10 cm.
Exercice 25 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une lourde machine pesant 300 kg est placée sur un support antivibratoire. La déformation statique $\gamma$ des fondations due au poids de la machine est de 7.5 cm.
Quand la base des fondations est sujette à une oscillation harmonique, à la fréquence propre, $S\left(t\right)=s_0 \sin \hspace{0.17em}{\omega }_0\hspace{0.17em}t$, on observe que la machine vibre avec une amplitude $A_0$ de 1 cm ( c'est-à-dire), en négligeant l'amortissement, à la résonance ${\omega }_r={\omega }_0$ ou $r=\frac{{\omega }_r}{{\omega }_0}=1$).











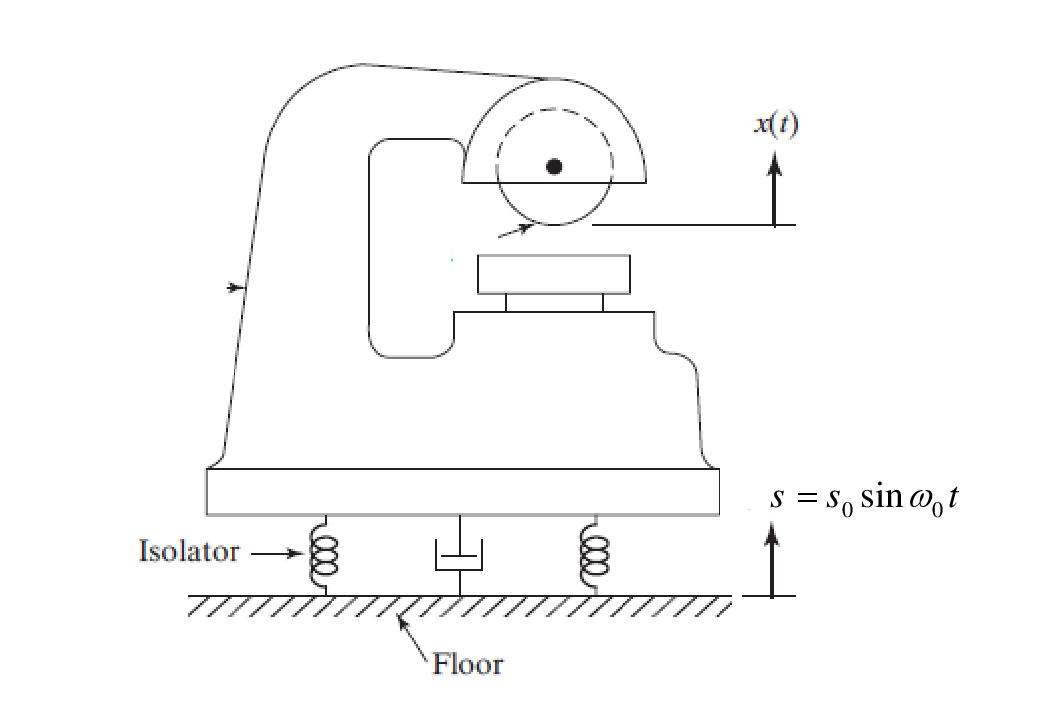
1. Exprimer la condition d'équilibre. En déduire la valeur de la constante de raideur du ressort.
2. Établir l'équation du mouvement. En déduire que l'amplitude de la force dynamique de la base Fr présente deux composantes.
3. Après avoir trouvé la constante d'amortissement des fondations (coefficient d'amortissement), donner la réponse du système en régime permanent. En déduire l'amplitude du déplacement relatif de la machine par rapport à la base Z(t)= x(t)-s(t).
Données : $g=10m/s^2, X_{eq}=7.5cm, X = 1cm quand S_0=0.25cm$.
Exercice 26 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
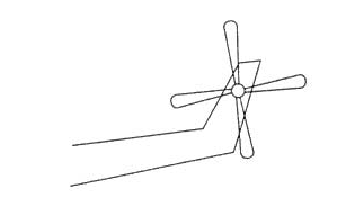
La section du rotor de queue de l'hélicoptère de la figure se compose de quatre pales d'une masse de $m_e=2,3kg$ et d'un carter moteur de 28,5 kg. Le centre de gravité de chaque barre est à l=170 mm de l'axe de rotation.
La queue est reliée au corps principal du hélicoptère par une structure élastique.
La fréquence naturelle de la queue est de 135 rad / s. En vol, le rotor fonctionne à 900 tr / min.











1. Calculer la pulsation propre de vibration de la queue si l'une des pales tombe pendant le vol? Supposons un rapport d'amortissement de 0,05.
2. Existe il un risque de résonance dans ce cas
Exercice 27 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Concevez une colonne en acier circulaire creuse de poids minimal pour le réservoir d'eau illustré à la figure











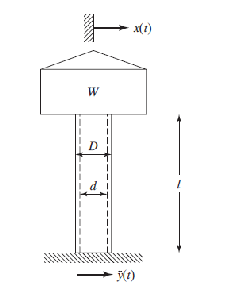
Le poids du réservoir (W) est de 45359,237 kg et la hauteur est de 15,24 m. La contrainte induite dans la colonne ne doit pas dépasser la limite d'élasticité du matériau, soit $32,06843\hspace{0.17em}{10}^8\hspace{0.17em}pascal$, lorsqu'elle est soumise à une accélération harmonique du sol (due à un séisme) d'amplitude 0,5 g et de fréquence 15 Hz.
Supposons un rapport d'amortissement de 0,15 pour la colonne.
Exercice 28 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Une pompe alternative pesant 75 Kg est montée au milieu d'une plaque d'acier de 13 mm d'épaisseur, de largeur 500 mm et de longueur 2.5 m. Serrée le long de deux bords, comme illustré à la figure.











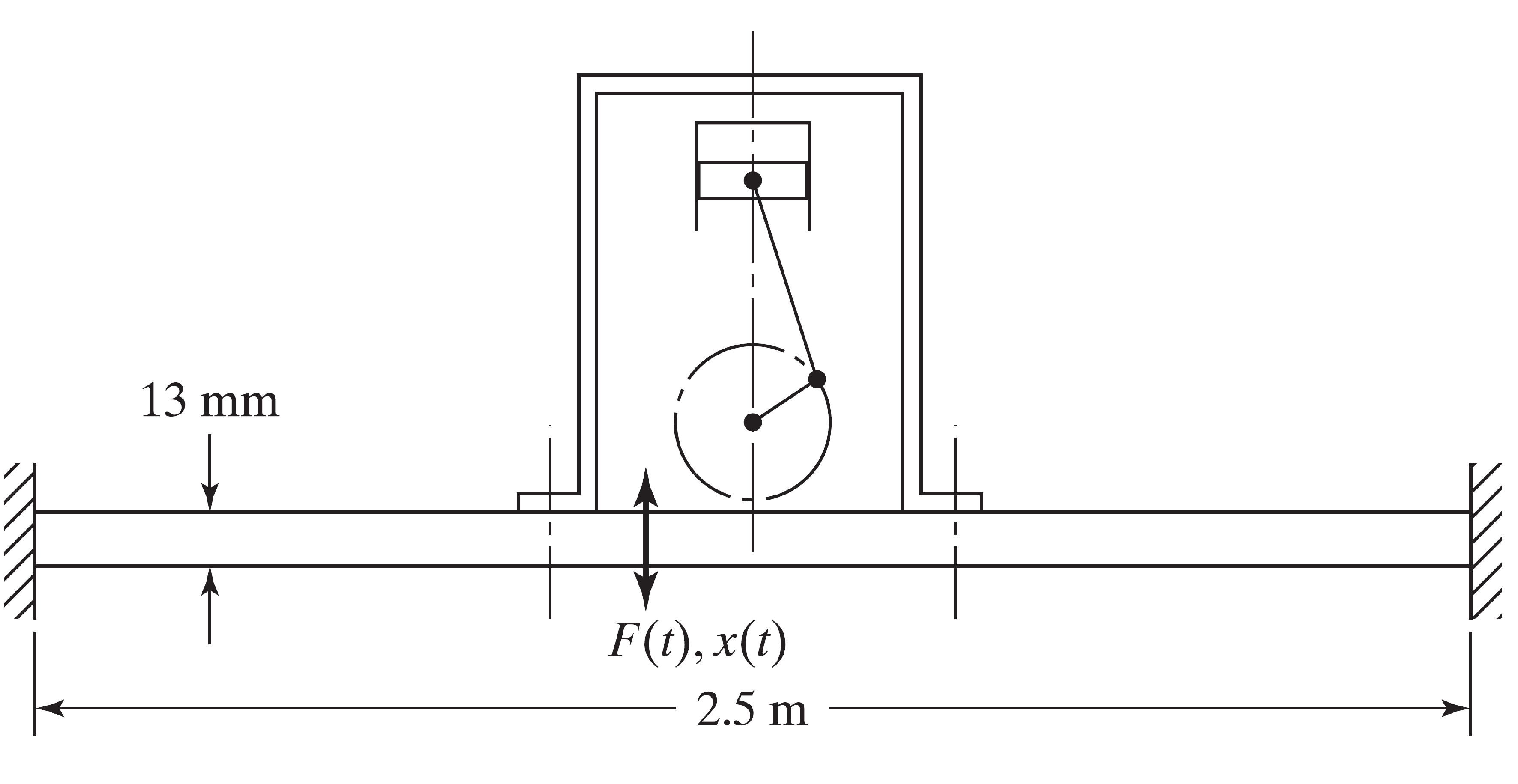
Pendant le fonctionnement de la pompe, la plaque est soumise à un effort harmonique : $F\left(t\right)=250 \cos (62.8\hspace{0.17em}t)\hspace{0.17em}N$.
Trouver l'amplitude de vibration de la plaque.
On donne : $k=\frac{192\hspace{0.17em}E\hspace{0.17em}I}{l^3}$ avec : E= 200 Gpa
Exercice 29 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
On constate qu'un moteur électrique de masse M, monté sur une base élastique, vibre avec une déviation de 0,15 m à la résonance











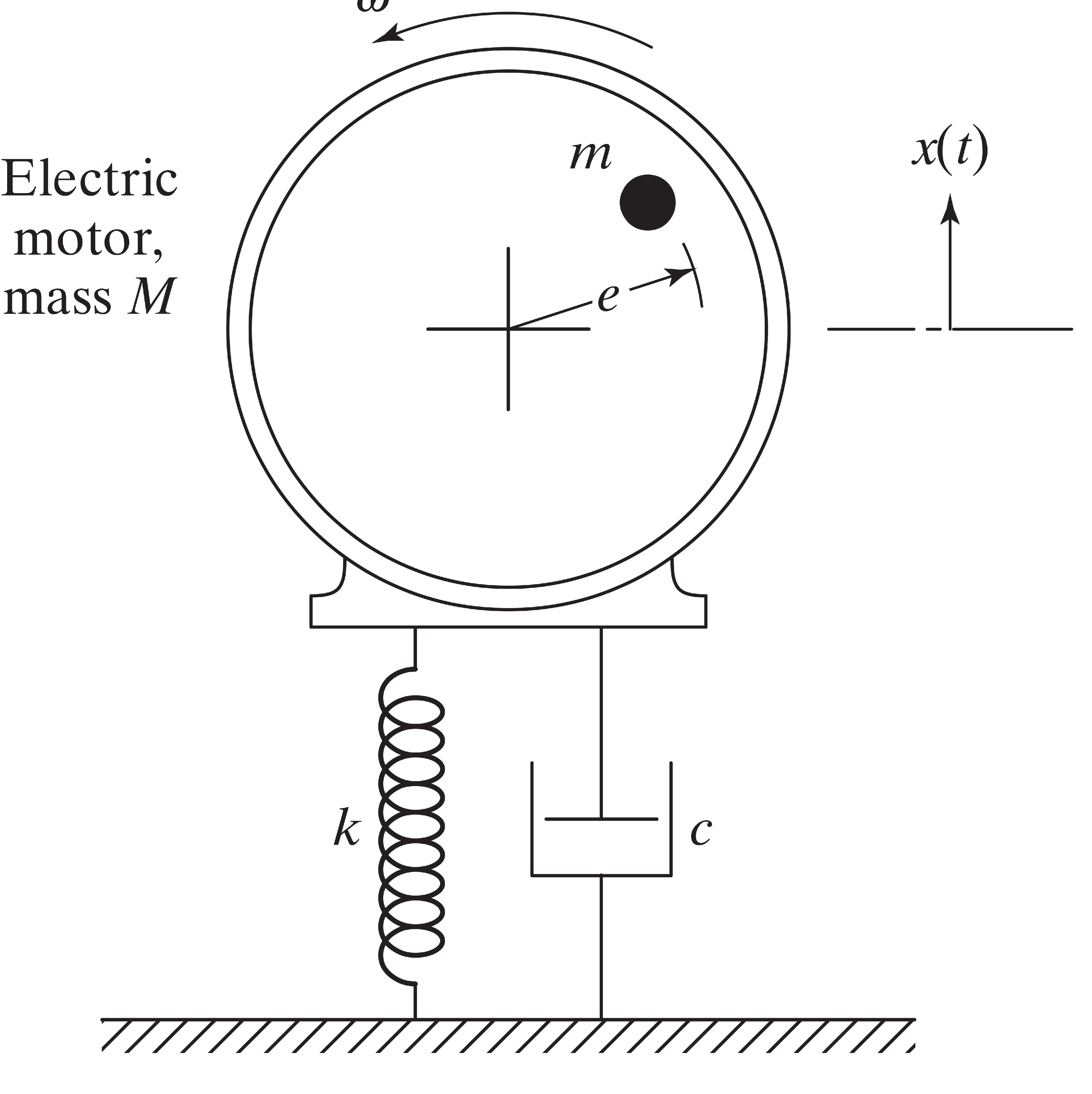
On sait que la masse non équilibrée du moteur est égale à 8 % de la masse du rotor due aux tolérances de fabrication utilisées. Le taux d’amortissement de la fondation est 0.025. Déterminer ce qui suit:
1. L'excentricité ou la localisation radiale (e) de la masse du balourd .
2. La masse supplémentaire à ajouter uniformément au moteur si l'amplitude des vibrations à la résonance doit être réduit à 0,1 m.
Exercice 30 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
La figure est un diagramme schématique d'une turbine à eau Francis dans laquelle l'eau s'écoule de A dans les aubes B et descend dans la piste de queue C.











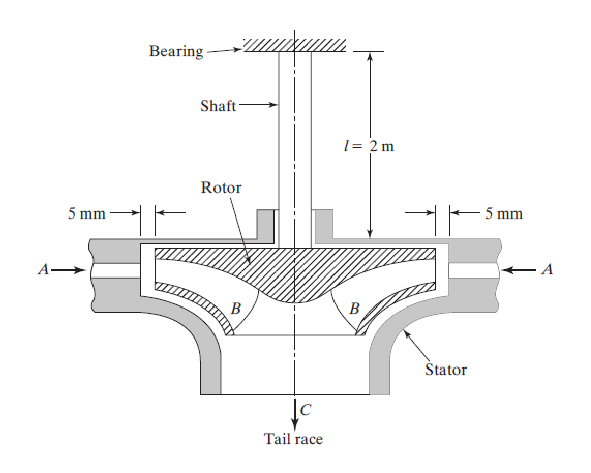
Le rotor a une masse de 250 \: kg et un balourd ($m_e$) de 5 kg mm. Le jeu radial entre le rotor et le stator est de 5 mm.
La turbine fonctionne dans la plage de vitesses allant de 600 à 6000 tr / min. On peut supposer que l'arbre en acier portant le rotor est encastré au niveau des paliers.
Déterminer le diamètre de l'arbre de sorte que le rotor soit toujours dégagé du stator à tous les vitesses de fonctionnement de la turbine. Supposons que l'amortissement soit négligeable.
On donne : $E=2.{0710}^{11}$
$k = \frac{3 E}{l^3}\hspace{0.17em}\left(\frac{4 \pi d^4}{64}\right)$
Exercice 31 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
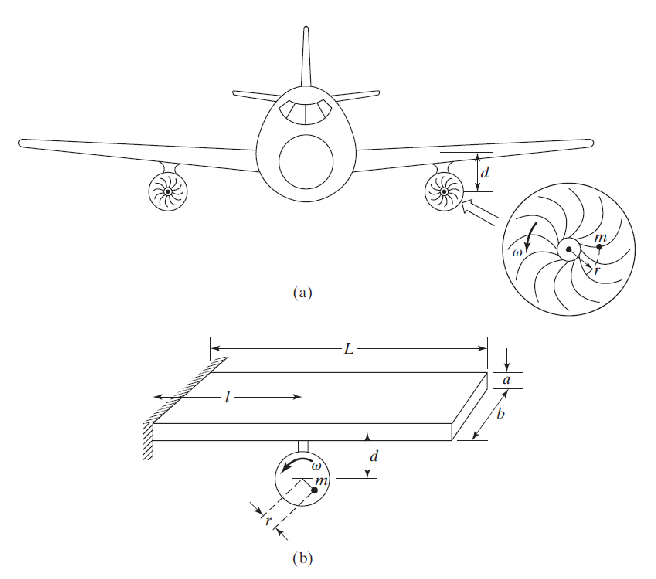
Un moteur d'avion a une masse déséquilibrée en rotation $m$ au rayon $r$. Si l'aile peut être modélisée comme une poutre en porte à faux de section transversale uniforme comme représenté sur la figure (b), déterminer l'amplitude maximale des vibrations du moteur à une vitesse $N$. Supposons que l’amortissement et l’effet de l’aile entre le moteur et l’extrémité libre soient négligeables.
On donne : $k = \frac{ E b a^3}{4 l^3}$.
















Exercice 32 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
L'actionneur à ressort illustré à la figure fonctionne en utilisant la pression d'air d'un contrôleur pneumatique (p) comme entrée et en fournissant un déplacement de sortie à une vanne (x) proportionnelle à la pression d'air. Le diaphragme, constitué d’un caoutchouc à base de tissu, a une zone A et dévie sous la pression d’air d’entrée contre un ressort de raideur k.
On donne : $k = \frac{ E b a^3}{4 l^3}$.













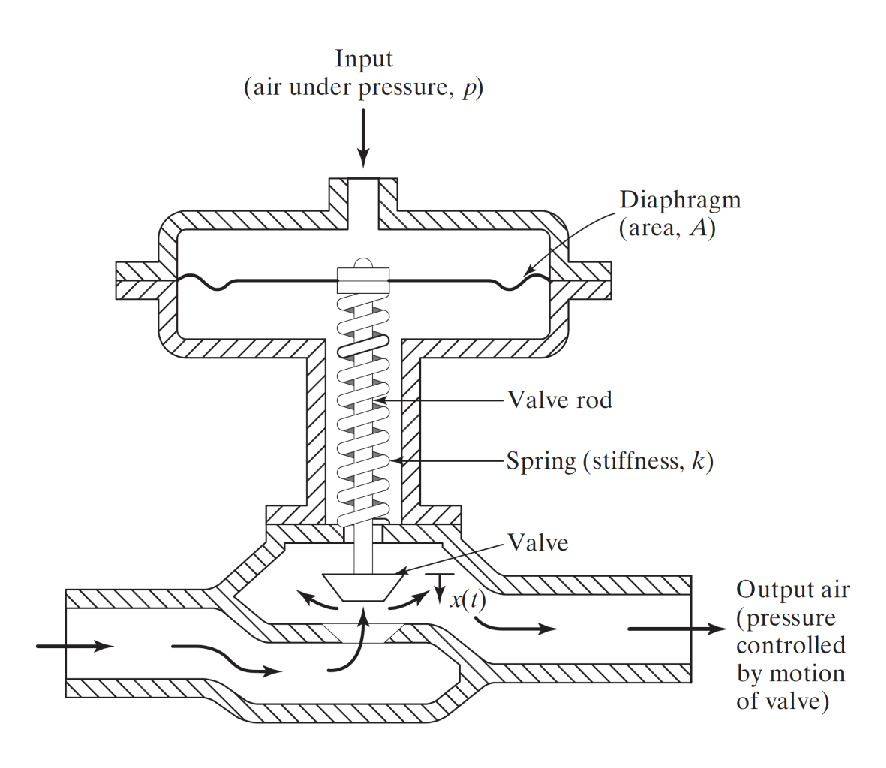
Calculer l'amplitude de vibration de la vanne sous une pression d’air d’entrée fluctuant harmonieusement $p\left(t\right)=p_0 sin\hspace{0.17em}\omega \hspace{0.17em}t$ pour les données suivantes:
$p_0$ = 65 kPa, $\omega$ = 8 rad / s, la section A = 0.065 $m^2$, $k=75\times \hspace{0.17em}{10}^3 N/m$, poids du ressort = 8 Kg et poids de la vanne et de la tige de la vanne = 12 Kg.
Exercice 33 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Un moteur d'automobile à quatre cylindres doit être supporté par trois supports d'amortisseur, comme indiqué à la Figure.













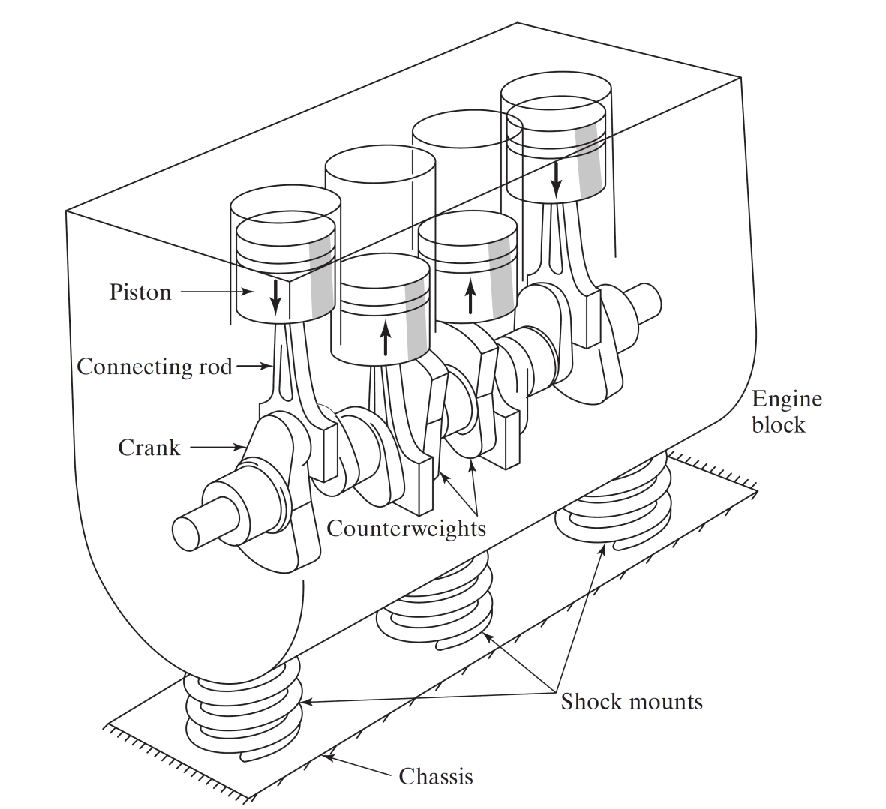
Le bloc moteur pèse 250 Kg. Si la force non équilibrée générée par le moteur est donnée par $1000 \sin \hspace{0.17em}100\hspace{0.17em}\pi \hspace{0.17em}t$ N , concever les trois supports d’amortisseur (de rigidité k et de constante c), de sorte que l’amplitude de vibration est inférieure à 25 mm. On pose que $\zeta =0.01$
Exercice 34 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
L'hélice d'un navire, d'un poids de ${10}^5$ N et d'un moment d'inertie de masse polaire de 10000 kg $m^2$, est reliée au moteur par un arbre d'hélice creux en acier renforcé, comme indiqué à la Figure.













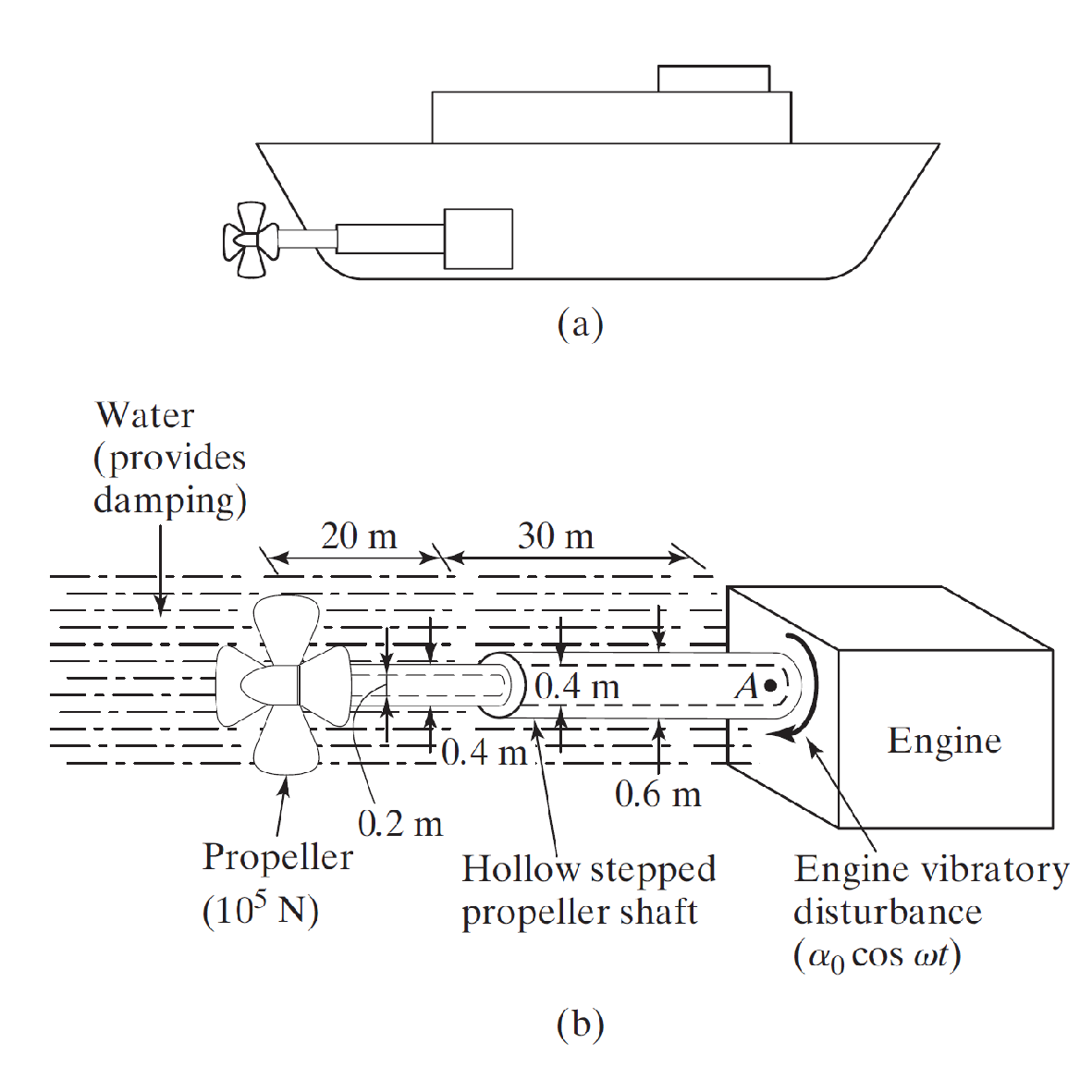
En supposant que l’eau fournisse un rapport d’amortissement visqueux de 0,1, déterminer la réponse vibratoire en torsion de l’hélice lorsque le moteur induit un déplacement angulaire harmonique de 0,05 sin. 314,16 t rad à la base (point A) de l’arbre de transmission.
On donne : $k_t=\frac{80\pi \left(\left(d_e^4-d_i^4\right)\right)}{32 \ell }\times {10}^9$
Avec $d_e$ est le diamètre extérieur et $d_i$ est le diamètre inférieur.
Exercice 35 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Une caméra vidéo, d'une masse de 2,0 kg, est montée au sommet d'un bâtiment de banque pour la surveillance. La caméra vidéo est fixée à une extrémité d'une tige tubulaire en aluminium dont l'autre extrémité est fixée au bâtiment, comme indiqué à la Figure.













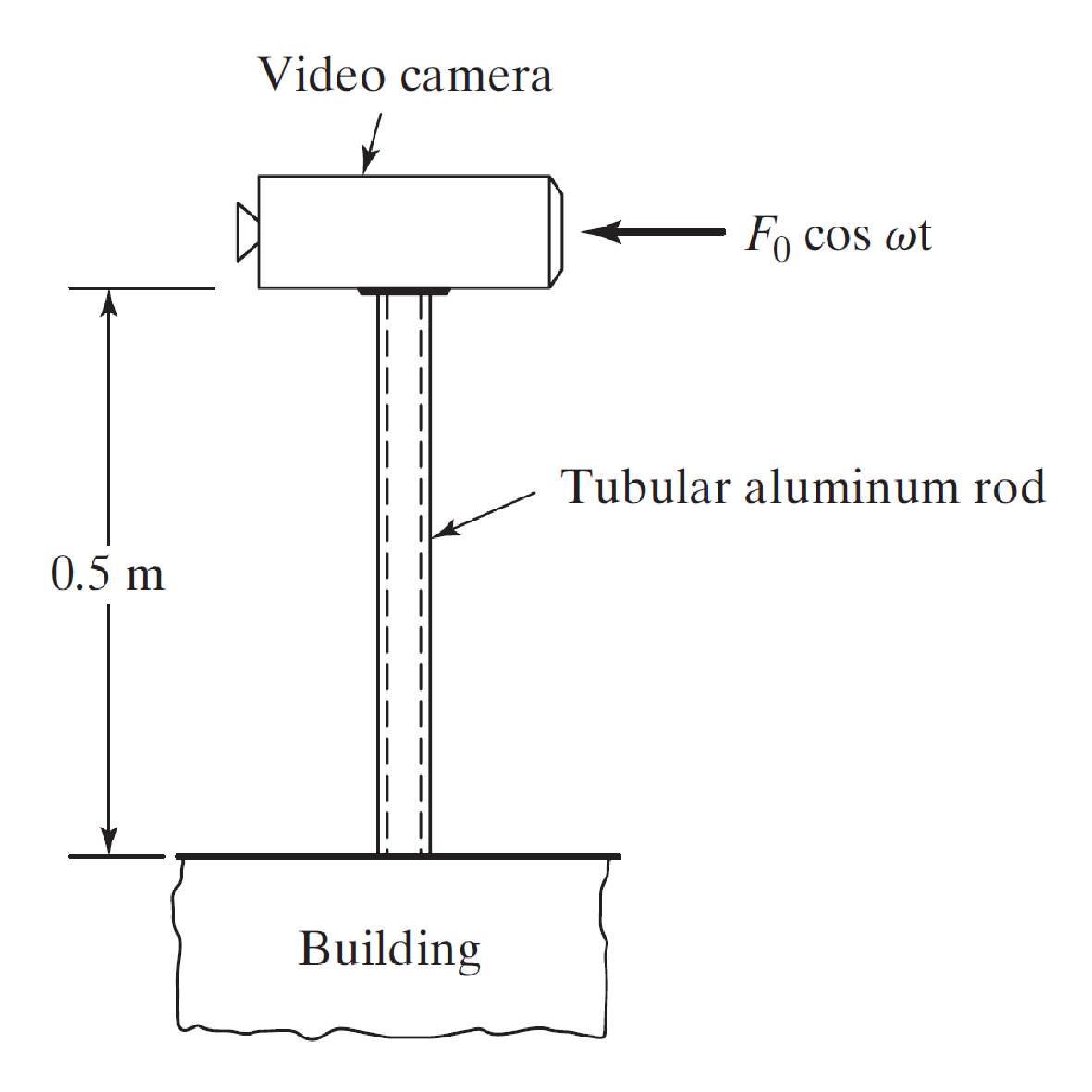
La force induite par le vent agissant sur la caméra vidéo, f (t), s’avère être harmonique avec $f\left(t\right)=25\hspace{0.17em} cos\hspace{0.17em}75.3984\hspace{0.17em}t$ N. Déterminer les dimensions de la section transversale du tube en aluminium si l'amplitude maximale de vibration de la caméra vidéo doit être limitée à 0,005 m. On donne : $k=\frac{{\displaystyle 3 E I}}{{\displaystyle {\ell }^3}}$ Avec : E=71 Gpa; et $I=\frac{{\displaystyle \pi }}{{\displaystyle 64}}\left(d_e^4-d_i^4\right)$
On pose que $\frac{{\displaystyle d_e}}{{\displaystyle d_i}}=10$

Exercice 36 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
Le train d'atterrissage d'un avion peut être idéalisé en tant que système masse - ressort -amortisseur illustré à la Fig. 4.60. Si la surface de la piste est décrite, $y\left(t\right)=y_0 \sin \hspace{0.17em}\omega \hspace{0.17em}t$.













Si $k=5\hspace{0.17em}\times \hspace{0.17em}{10}^6$, déterminer la valeur de c qui limite l'amplitude de vibration de l'avion (x) à 0,1 m. Supposons que: m = 2000 kg, $y_0$ = 0,2 m et $\omega =157.08$ rad / s

Exercice 37 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019 )
L'une des pales du rotor de queue d'un hélicoptère a une masse non équilibrée de 0,5 kg à une distance de e = 0,15 m de l'axe de rotation, comme indiqué sur la figure.













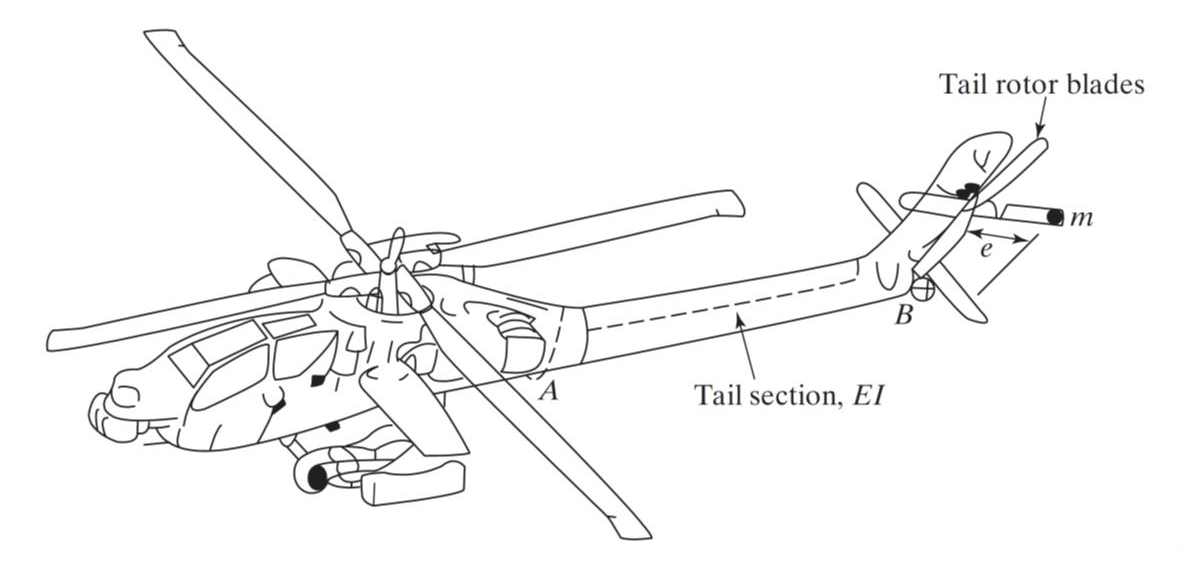
La section de la queue a une longueur de 4 m, une masse de 240 kg, une rigidité en flexion (E I) de 2,5 MN- $m^2$ et un coefficient d'amortissement de 0,15. La masse des pales du rotor de queue, y compris leur système d’entraînement, est de 20 kg.
Déterminer la réponse forcée de la queue lorsque les pales tournent à 1500 tr / min.
On donne $k=\frac{3 E I}{{\ell }^3}$