Exercice 1.
La figure représente un disque qui peut osciller atour de son axe horizontal fixé à O. Une tige de masse m et de longueur l est soudée au disque comme l’indique la figure. On donne $\left|oA\right|=\frac{R}{2}$.
Établir l’équation différentielle du mouvement et déduire la pulsation propre et le facteur d’amortissement.

Exercice 2
La figure représente un cylindre homogène de masse 2M et de rayon R qui peut osciller atour de son axe horizontal fixé à O. On soude perpendiculairement à son axe une tige de longueur l et de masse négligeable. L’autre extrémité est fixée à un ressort de raideur k et un amortisseur de coefficient d’amortissement c.
1. Pour des faible oscillations, Etablir l’équation différentielle du mouvement et déduire la pulsation propre et le facteur d’amortissement.
2. Sachant que La période des oscillations est de 1s, et que l’amplitude des oscillations chute de moitié après 5 oscillation, calculer k et c. On donne M=5kg, R=0.2 m et l=2m. Exercice 3
Dans la figure la tige de masse 2 m et de longueur 4 l peut osciller atour de son axe horizontal fixé à O.
1. Pour des faibles oscillations, établir l’équation différentielle du mouvement et déduire la pulsation propre ainsi que le facteur d’amortissement.




Exercice 4
Le système de la figure est constitué d’un disque homogène de rayon R oscillant autour de son axe fixe O, est relié à un bâti par un amortisseur de coefficient c.
Une masse m est fixée d’une part au disque et fait un mouvement oscillatoire avec son mouvement et d’autre part à un ressort de raideur k. On donne oA = R/2.
1. Pour des faibles oscillations, établir l’équation différentielle du mouvement et déduire la pulsation propre ainsi que le facteur d’amortissement.
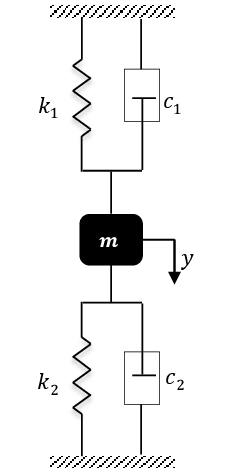
Exercice 5
1. Pour le système de la figure, établir l’équation différentielle du mouvement et déduire la pulsation propre ainsi que le facteur d’amortissement.
2. Pour chacun des cas suivant, déduire la nature du mouvement :
(a) M=2 Kg, k_1=50N/m , k_2=40N/m, c_1=0.3Ns/m , c_2=0.2 Ns/m.
(b) M=2 Kg, k_1=23N/m , k_2=27N/m, c_1=8 Ns/m, c_2=12 Ns/m.
(c) M=2 Kg, k_1=1.5N/m, k_2=0.5N/m, c_1=5.5 Ns/m, c2=2.5 Ns/m.
2. Écrire l'équation horaire y(t), sachant que à t=0 : y(0)=1 cm et la vitesse -6 cm/s.

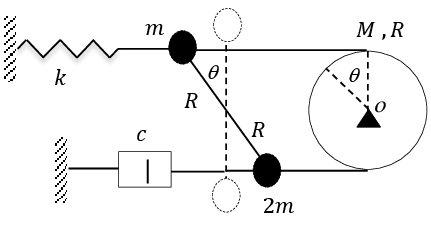
Exercice 6
1. Pour le système de la figure, établir l’équation différentielle du mouvement et déduire la pulsation propre et le facteur d’amortissement.
2. Sachant que m=2Kg, M=5Kg, k=0.4 N/m, R=50 cm, g=10 m/s., trouver la valeur maximale que c ne doit pas atteindre pour que le système oscille.
3. Avec une valeur de c=20 Ns/m le système oscille, mais son amplitude diminue au cours du temps. Trouver le temps nécessaire pour que l’amplitude diminue à 1/5 de sa valeur.
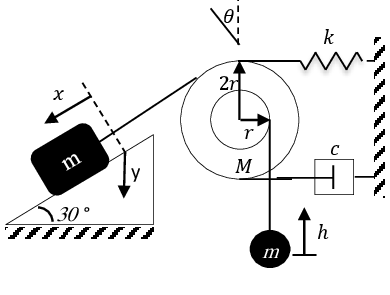
4. L’amortisseur précédent est maintenant remplacé par un autre amortisseur de coefficient c’, on remarque alors que l’amplitude diminue de 1/3 de sa valeur après 24 oscillation complètes. Calculer la valeur de c’. Exercice 7
Un disque de masse M et de rayon 2 r, est relié à sa périphérique à un ressort de raideur k et à un amortisseur c. une masse m, posée sur un plan incliné, est reliée à la périphérie du disque par un fil. Une autre masse m est suspendue à un fil enroulé autour d’un sillon de rayon r gravé sur la surface du disque. Les fils sont inextensibles et non glissants. Le disque peut tourner librement autour de son axe horizontal fixe.
1. Etablir l’équation différentielle du mouvement.
2. Sachant que c=21Ns/m ;k=7N/m et m=M=1kg ; trouver la nature du mouvement.
3. Quelle est la valeur de c qui ne faut pas dépassée pour avoir des oscillations.
4. Si c=2 Ns/m, calculer le temps au bout duquel l’amplitude est divisée par 5.
Exercice 8 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un cycliste peut être modélisé par un système masse-ressort-amortisseur avec un poids, une raideur et une constante d'amortissement de 800 N, 50000 N/m et 1000 N.s/m, espectivement.
Une pause différentielle de blocs de béton sur l'autoroute a causé le niveau de la surface de diminuer soudainement comme l'indique la figure













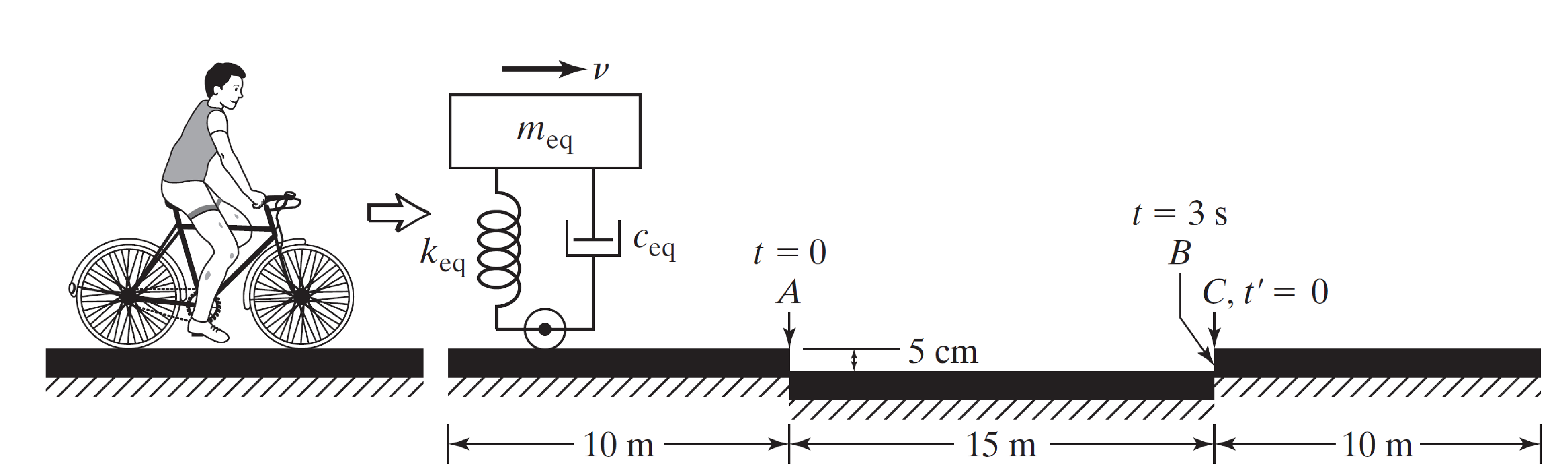
1. Si la vitesse de la bicyclette est de 5 m/s (18km/h) déterminer le déplacement du cycliste dans la position verticale, supposez que la bicyclette était libre de toute vibration avant de subir ce changement dans la direction verticale.
2. Ecrire la solution sous la forme $y\left(t\right) = A e^{-\lambda t} \cos ({\omega }_a t + \varphi )$. Où $\omega_a$ est la pulsation des oscillations amorties.
Exercice 9 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Soit l’équation différentielle du mouvement suivante : $m\ddot{x}+c\dot{x}+kx=0$
1. Soit $x\left(t\right)=A{e}^{-\beta t}{e}^{i\omega t}{e}^{\phi }$ une solution de cette équation différentielle du mouvement.
Déterminer $\beta$ en fonction de m et c.
2. Sachant que la pseudo période des oscillations est de $\pi /3\hspace{0.17em}s$. Déterminer la valeur de c.
On donne m=1 kg et k= 100 N/m.
Exercice 10 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Soit un système libre amorti dont l’équation différentielle du mouvement est donnée par: $3 \ddot{x} +30 \dot{x} + 75 x =0$
1. Déterminer la nature du mouvement.
2. Pour t=0, on donne $x\left(0\right)=0 ;\dot{x}\left(0\right)=V_0=10m/s$, déterminer la solution générale de l’équation différentielle du mouvement.
Exercice 11 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Soit un système oscillatoire dont la solution de l’équation différentielle du mouvement est donnée par :$x\left(t\right)=6 e^{-0.3t} \cos (2\pi t + \phi )$
1. Déterminer la valeur de la pulsation propre.
2. Trouver la valeur de l’amplitude des oscillations après 6 oscillations. (trouver $x(t_0+6\hspace{0.17em}{T}_a)$, avec $t_0=0$.)
Exercice 12 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Le système montré dans la figure a une fréquence naturelle de 5 Hz. Pour les données suivantes : M = 10 Kg$, Jo = 5 Kg m^2, r_1=10 cm, r2 = 11 cm, quand le système subit une perturbation qui lui donne un déplacement initial, l'amplitude de vibration libre est réduite de 80 % en 10 périodes.













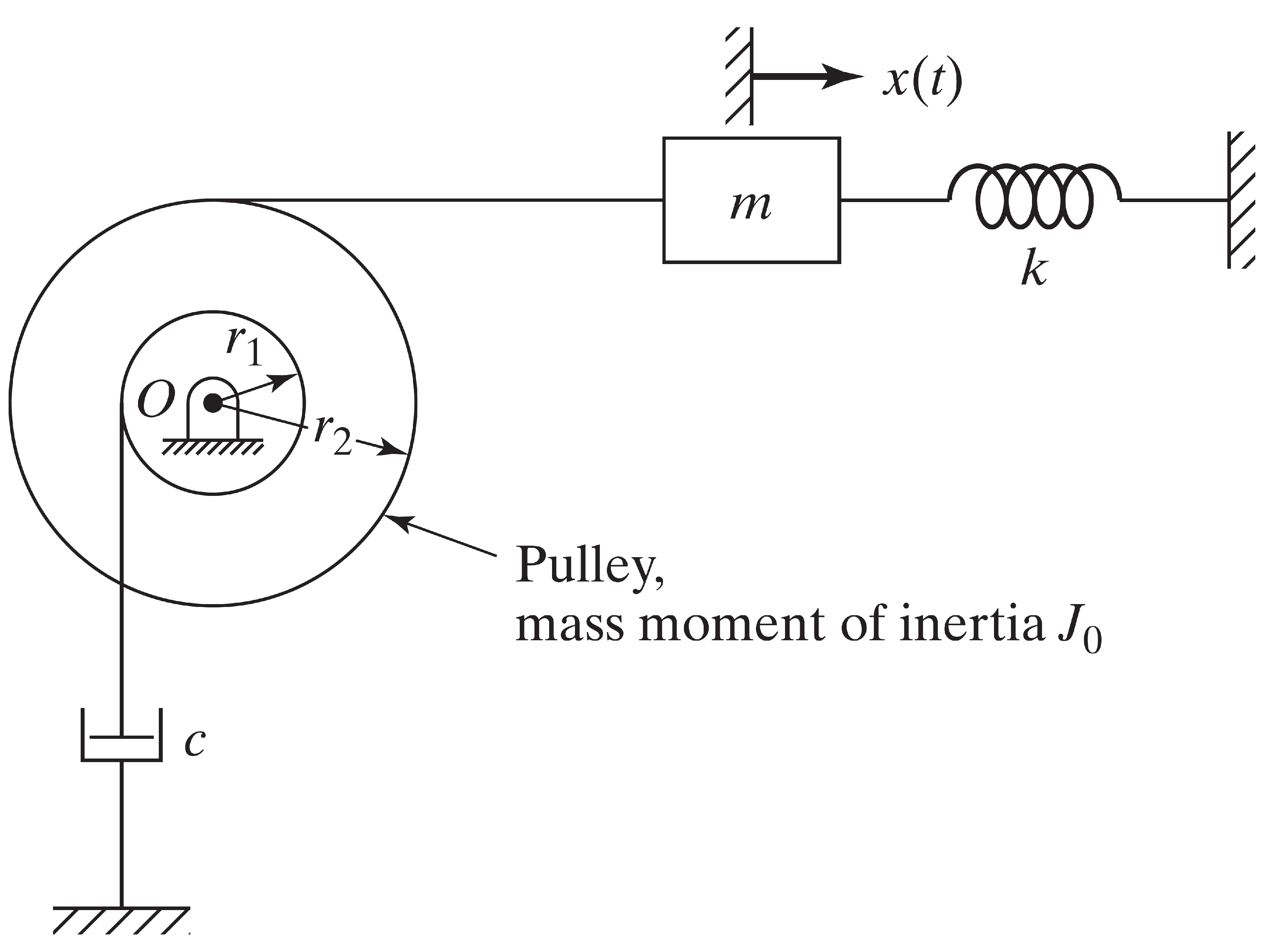
Déterminer les valeurs de k et de c
Exercice 13 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Le graph de la figure, représente la courbe de déplacement de la masse m en fonction du temps pour un cas d’un mouvement à amortissement critique.
La masse m étant connue (1 Kg), on cherche à identifier la suspension (c.à.d trouver k et c).











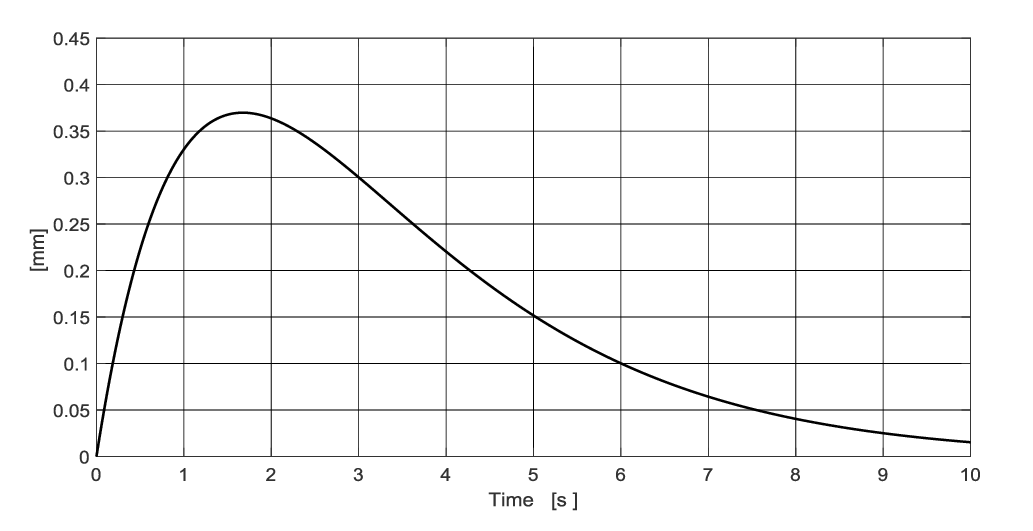
Déterminer les valeurs de k et de c
Exercice 14 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Le schéma simplifié d'un canon est montré sur la figure.
Quand le canon tire un boulet, des gaz de haute pression accélèrent le projectile à l'intérieur d'un baril à une vitesse très élevée.
La force de réaction qui en résulte pousse le baril dans la direction opposée du projectile.











Puisqu'il est désirable de ramener le baril dans la position fixe dans le temps le plus court sans oscillations, on utilise l'amortissement critique d'un système masse-ressort-amortisseur qu'on appelle le mécanisme de rappel. La distance maximum de rappel du canon est spécifiée comme étant 0.5 m. Si la vitesse initiale de rappel est 10 m/s et la masse du canon est 500 kg.
Trouver la constante de raideur du mécanisme de rappel ?
Exercice 15 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
On donne m=1 kg et k= 100 N/m.











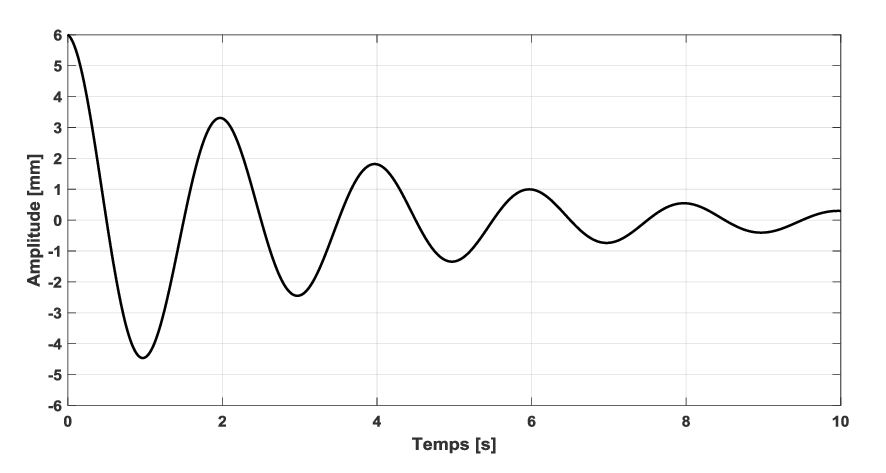
1. A partir de la figure déterminer la valeur du facteur d’amortissement.
2. Déterminer la valeur de c.
3. Déterminer la pulsation propre.
Exercice 16 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
La réponse des oscillations libres d'un moteur électrique de poids 500 N, monté sur des fondations est montrée sur la figure.











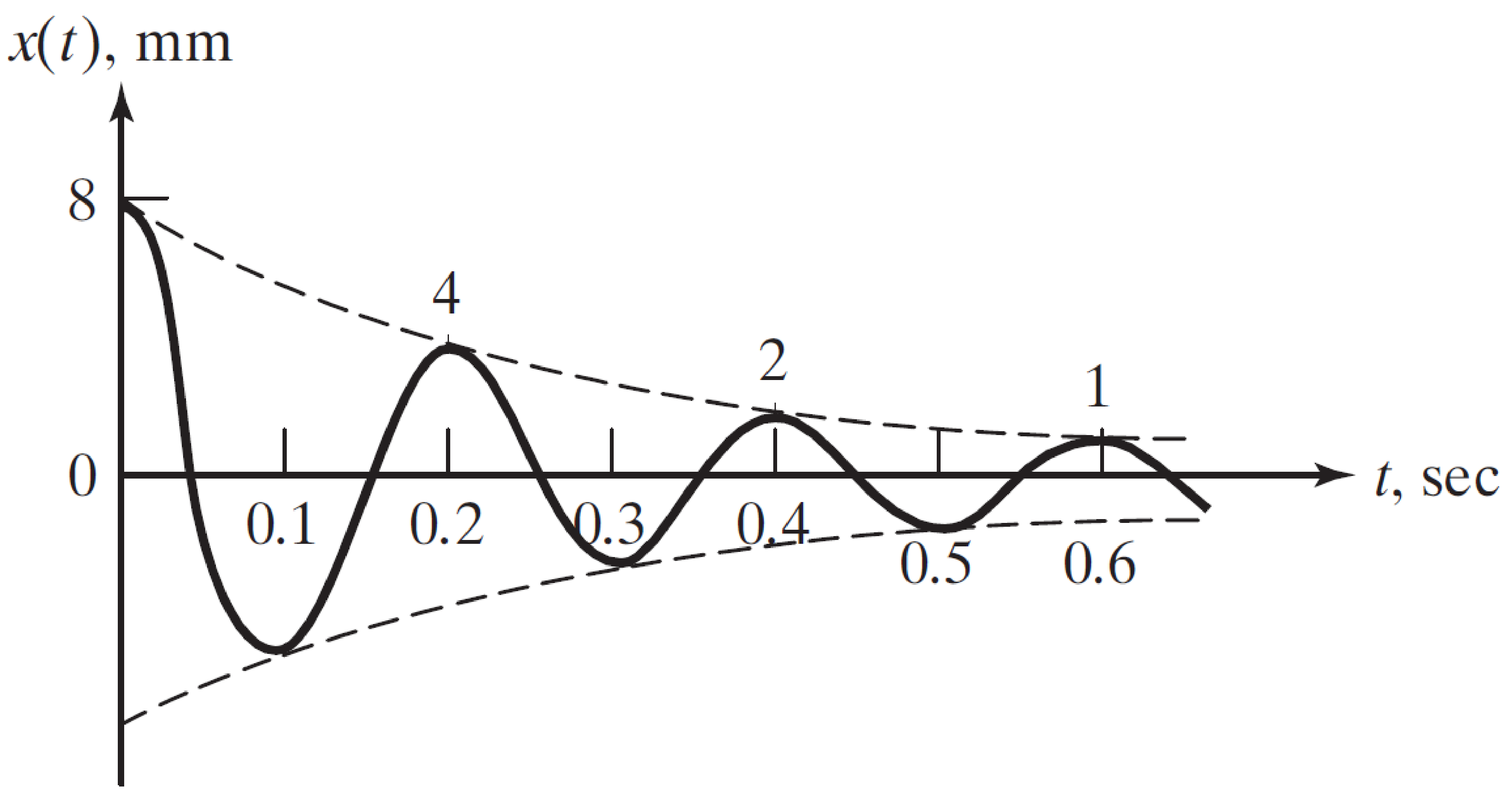
Trouver le coefficient d'amortissement des fondations et la raideur du ressort des fondations.
Exercice 17 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
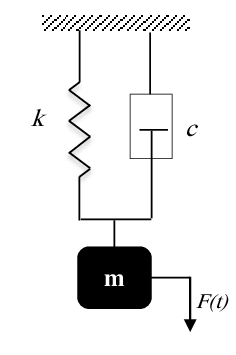
Un amortisseur sous amorti doit être conçu pour une motocyclette d’une masse de 200 kg (figure(a)).
Lorsque l'amortisseur est soumis à une vitesse verticale initiale due à un choc sur la route, la courbe de déplacement en fonction du temps qui en résulte doit être celle indiquée à la figure(b)











1. Déterminer les constantes de rigidité et d’amortissement nécessaires de l’amortisseur si la période de vibration atténuée doit être de 2 s et que l’amplitude doit être réduite à un quart par demi-cycle (c.-à-d.$x_{1.5}=x_1/4$).
2. Trouver également la vitesse minimale initiale qui conduit à un déplacement maximal de 250 mm.
Exercice 18 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un wagon de chemin de fer d'une masse de 2 000 kg se déplaçant à une vitesse v = 10 m / s est arrêté au bout des voies par un système d'amortisseur à ressort, comme illustré à la Figure.











Déterminer le déplacement maximum du wagon après l’engagement des ressorts et de l’amortisseur.
On donne :
La raideur du ressort est k = 40000 N / m.
La constante d'amortissement est c = 17888.4 N-s / m.

Exercice 19 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
La figure présente un schéma du système de soupape et de culbuteur pour un moteur à combustion interne.











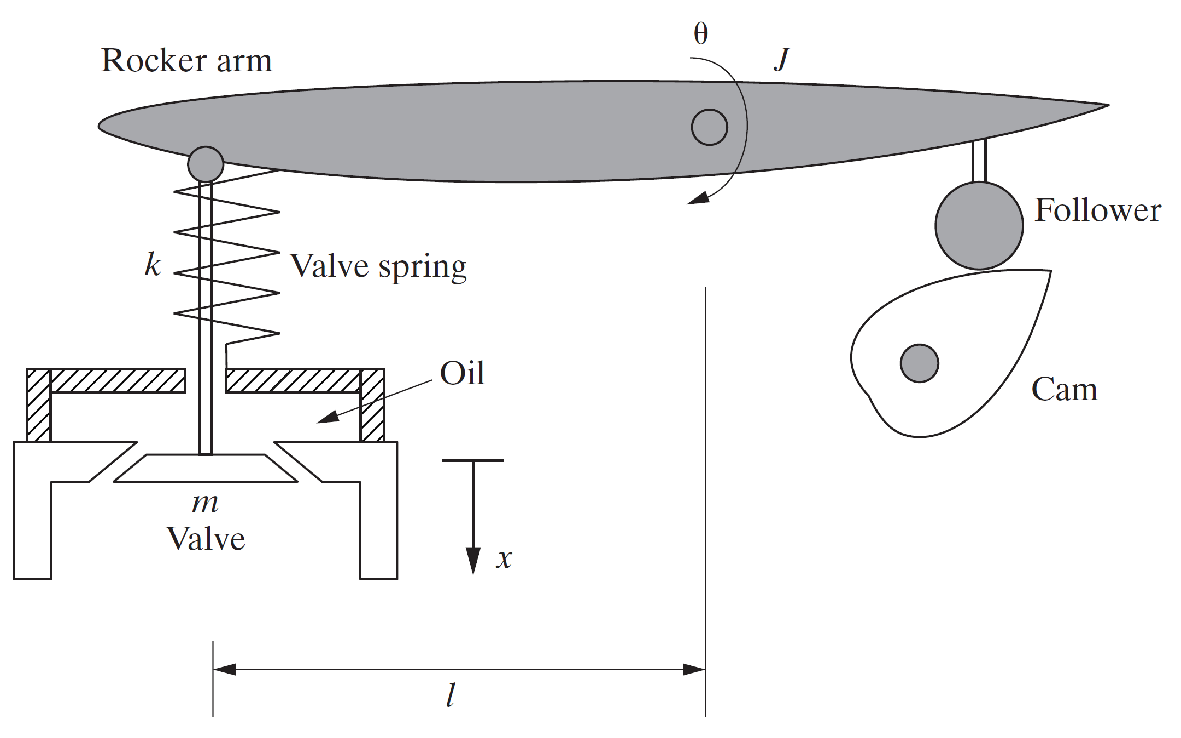
1. Modéliser le système sous la forme d'un pendule relié à un ressort et à une masse et supposer que l'huile a le rôle d'un amortissement visqueux de l'ordre de $\zeta$= 0,01.
2. Déterminer l'équation du mouvement et déterminer l'expression de la fréquence naturelle et de la fréquence naturelle atténuée.
Ici, J est l'inertie de rotation du culbuteur autour de son point de pivot, k est la raideur du ressort de soupape et m est la masse de la soupape et de la tige. Ne pas tenir compte de la masse du ressort.