Exercice 1.
Soit un oscillateur libre non amorti. Sa pulsation propre est de 1 rad/s. L’équation différentielle du mouvement régissant le déplacement x(t) est donc : $\ddot{x}+{\omega }_0^2\hspace{0.17em}=0$
Explicité x(t) dans les cas suivants :
1. L’amplitude est de 2 cm et, à t=0, x(0)=0 cm et la vitesse est positive.
2. x(0)=-1 cm et $\dot{x}\left(0\right)<0\hspace{0.17em}cm/s$ Exercice 2
Un oscillateur non amorti a pour caractéristiques m = 1 kg (masse) et k = 100N/m (raideur).
On le lance avec un écart initial $x_0=1\hspace{0.17em}cm$ et une vitesse $\dot{x}=2\hspace{0.17em}cm/s$.
Quelle sera l’amplitude du mouvement ? Exercice 3
La masse m de la figure, est fixée à l’extrémité d’une tige OA de longueur l et de masse négligeable. La tige est soudée au point « O » centre d’inertie d’un cylindre de masse M et de rayon R. Le cylindre peut rouler sans glisser sur un plan horizontal. A l’équilibre la tige est verticale. Pour des faibles oscillations :
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Déduire la pulsation propre des oscillations.



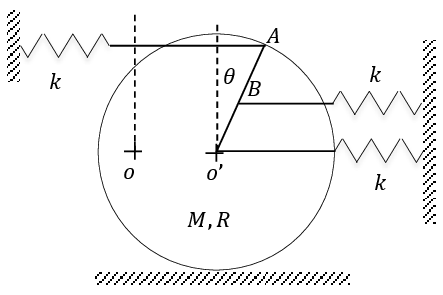
Exercice 4
Un cylindre homogène de masse $M$ et de rayon $R$ peut rouler sans glisser sur un plan horizontal. Trois ressort de raideur k sont fixés aux points O, A et B. tel que : $\left|OB\right|=\frac{R}{2}$.
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Établir l’équation différentielle du mouvement et déduire la pulsation propre des oscillations.

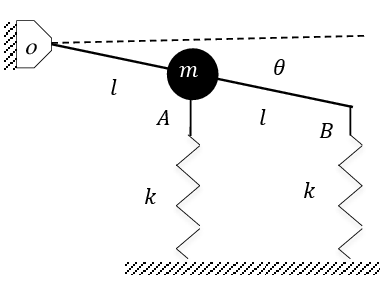
Exercice 5
Dans la figure, la masse de la tige OB est négligeable. A l’équilibre, la tige est horizontale, on ne s’intéresse qu’aux oscillations de faibles amplitudes.
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Déduire l’équation différentielle du mouvement et la pulsation propre des oscillations


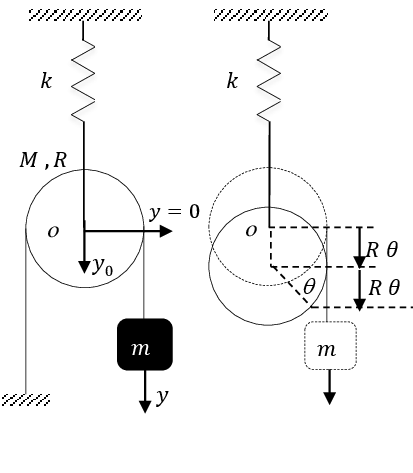
Exercice 6
Dans la figure, la corde qui maintient la masse m est inextensible et sans masse. Elle roule sans glisser sur la gorge de la poulie (de masse M et de rayon R).
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Déduire la pulsation propre des oscillations.




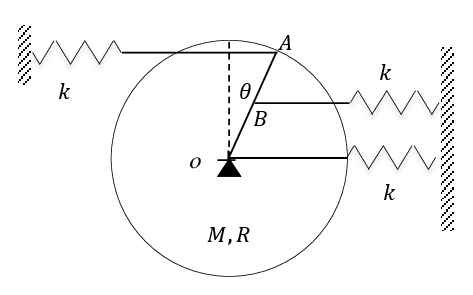
Exercice 7
Un cylindre homogène de masse $M$ et de rayon $R$ peut osciller autour de son centre d’inertie O. Trois ressorts de raideur k sont fixés aux points O, A et B tel que : |OB|=R/2 .
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Déduire l’équation différentielle du mouvement et la pulsation propre des oscillations.


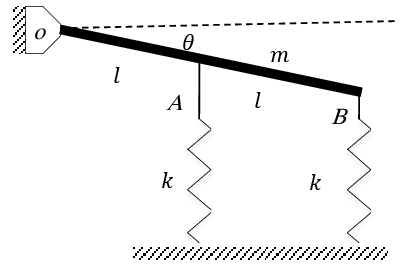
Exercice 8
Dans la figure, la tige OB est de masse m et de longueur 2 l. A l’équilibre, la tige est horizontale, on ne s’intéresse qu’aux oscillations de faibles amplitudes.
1. Trouver l’énergie cinétique et l’énergie potentielle du système.
2. Déduire l’équation différentielle du mouvement et la pulsation propre des oscillations.


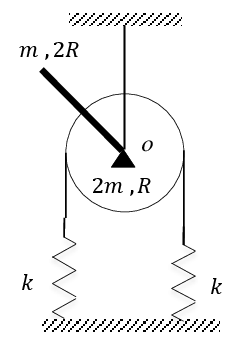
Exercice 9
Sur une poulie (cylindre creux)de masse 2m et de rayon R on soude une tige de masse $m$ et de longueur 2 R. La poulie est suspendue en son centre par une corde inextensible a un bâti fixe. De part et d’autre de la poulie on fixe sur sa périphérie deux ressorts de même raideur k. Les ressorts ont leur autre extrémité reliée au sol.
1. Déterminer la pulsation propre du système.



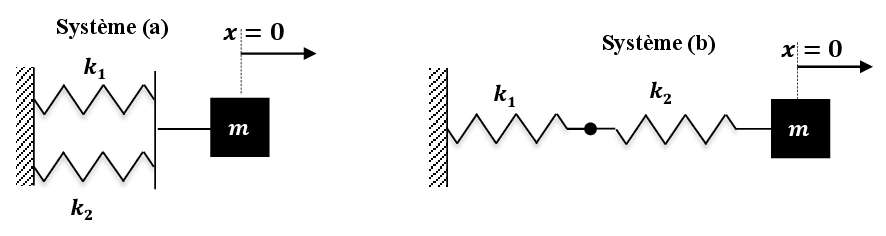
Exercice 10
Calculer l’énergie potentielle des systèmes a et b


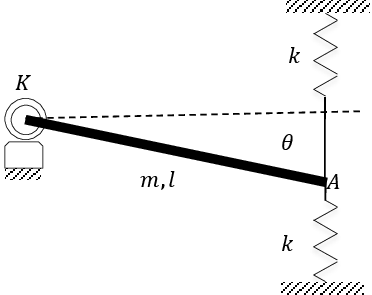Exercice 11
Dans la figure, la tige OB est de masse m et de longueur l. Elle est fixée à ses extrémités à un ressort en spirale K et deux ressorts identiques de raideur k. A l’équilibre, la tige est horizontale, on ne s’intéresse qu’aux oscillations de faibles amplitudes.
Déduire la pulsation propre des oscillations
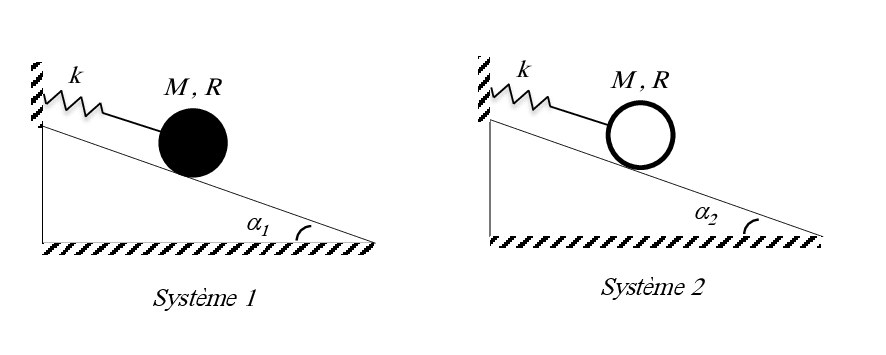Exercice 12
Soient les deux systèmes de la figure. 1er Système : un cylindre plein de masse M et de rayon R peut rouler sans glisser sur un plan incliné d’un angle ${\alpha }_1$ . Le cylindre est relié à un ressort de raideur k. 2ème Système : un cylindre creux de masse $M$ et de rayon extérieur $R$ peut rouler sans glisser sur un plan incliné d’un angle ${\alpha }_2$ . Le cylindre est relié à un ressort de raideur k.\\
1. Pour ${\alpha }_1$ = ${\alpha }_2$ Quel est le système qui possède la fréquence propre la plus petite ?.
2. Donner la relation entre ${\alpha }_1$ et ${\alpha }_2$ pour que les deux systèmes possèdent la même fréquence propre ?.
Exercice 13 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un cylindre de masse M de rayon R et de moment d'inetie Jo est libre de rouler sans glisser mais est retenu par deux ressorts de constante de raideur k1 et k2 comme le montre la figure.








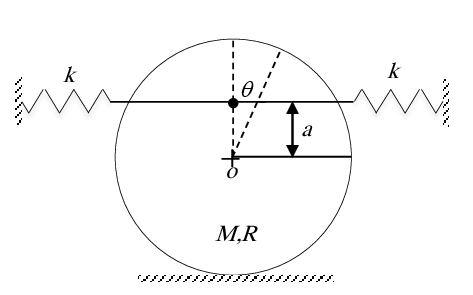
1. Trouver sa fréquence naturelle de vibration.
2. Trouver la valeur de $a$ qui maximise cette fréquence

Exercice 14 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un cylindre de masse M de rayon R est libre de pivoter au point O comme le montre la figure.








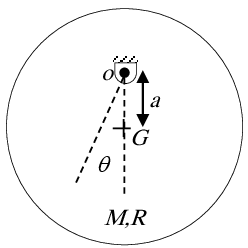
1. Trouver sa fréquence naturelle de vibration.
2. Trouver la valeur de $a$ qui maximise cette fréquence

Exercice 15 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un mécanisme de pédale pour une machine est modélisé comme un pendule relié à un ressort, comme illustré à la figure.
Le but du ressort est de maintenir la pédale à peu près horizontale.








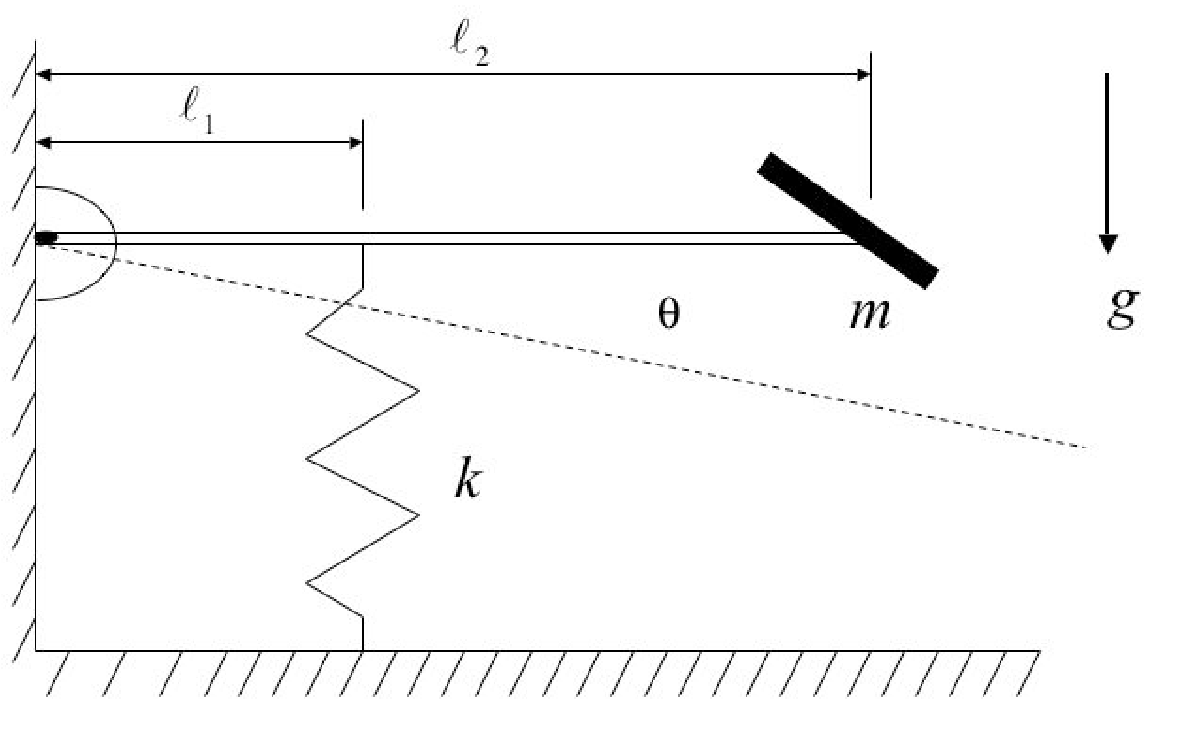
1. Calculer la raideur du ressort nécessaire pour maintenir le pendule horizontale, puis calculer la fréquence propre correspondante.
Supposons que les déviations angulaires soient faibles, de sorte que la déviation du ressort puisse être approximée par la longueur de l’arc, que la pédale puisse être traitée comme une masse ponctuelle et que la tige du pendule ait une masse négligeable.
Les valeurs sur la figure sont : m = 0,5 kg, $g = 9,8 m / s^2; {\mathcal{l}}_1= 0,2 m et {\mathcal{l}}_2= 0,3 m$ .
Exercice 16 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un homme de 120 kg est campé à l'extrémité du mât de drapeau de la figure.











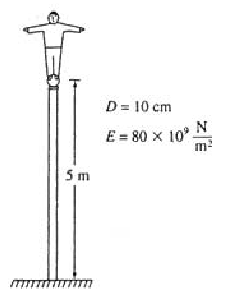
Calculer la fréquence propre des oscillations..
On donne : $K_0 =\frac{3E\hspace{0.17em}\pi D^4}{4\hspace{0.17em}{L}^3}$
Exercice 17 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
La colonne du réservoir d'eau représentée à la figure 2.24 (a) a une hauteur de $\mathcal{l}$=100 m et est en béton armé avec une section transversale tubulaire de diamètre intérieur d =2.5 m et de diamètre extérieur D =3 m.
Le réservoir pèse 275000 Kg lorsqu'il est rempli d'eau.
En négligeant la masse de la colonne et en supposant que le module de Young du béton armé est E = 30 Gpa, déterminer ce qui suit: .














1. La fréquence naturelle des vibrations transversales du réservoir d'eau.
2. La réponse vibratoire du réservoir d'eau due à un déplacement transversal initial de 25 cm.
3. Les valeurs maximales de la vitesse et de l'accélération subies par le réservoir d'eau.
On donne : $k = \frac{12 \pi E}{64 {\ell }^3}\left(D^4-d^4\right)$
Exercice 18 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Le cockpit d'un camion de pompier est situé à l'extrémité d'une perche télescopique, comme illustré à la Fig. 2.26 (a). Le cockpit et le pompier pèsent 2000 N.













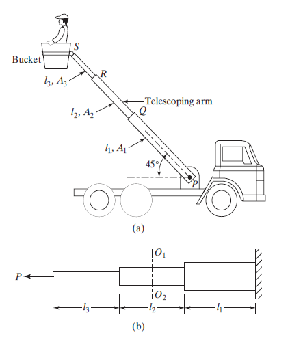
Trouver la fréquence naturelle des vibrations du cockpit dans le sens vertical.
On donne :
$$\begin{gathered} E=2.1\hspace{0.17em}{10}^{11}\hspace{0.17em}N/m^2; l_1=l_2=l_3=3m; A_1=20\hspace{0.17em}c{m}^2; A_2=10\hspace{0.17em}c{m}^2; A_3=5\hspace{0.17em}c{m}^2. \\ k = \frac{A E}{l} \end{gathered}$$
Exercice 19 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Une presse industrielle est montée sur un patin en caoutchouc pour l’isoler de sa fondation. Si le tampon en caoutchouc est comprimé de 5 mm par le poids propre de la presse, trouver la fréquence propre du système.

Exercice 20 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un chariot de mine chargé, pesant 2 000 Kg, est soulevé par une poulie sans friction et un câble métallique ($E=2\times {10}^{11}\hspace{0.17em}Pa$), comme illustré à la Figure.











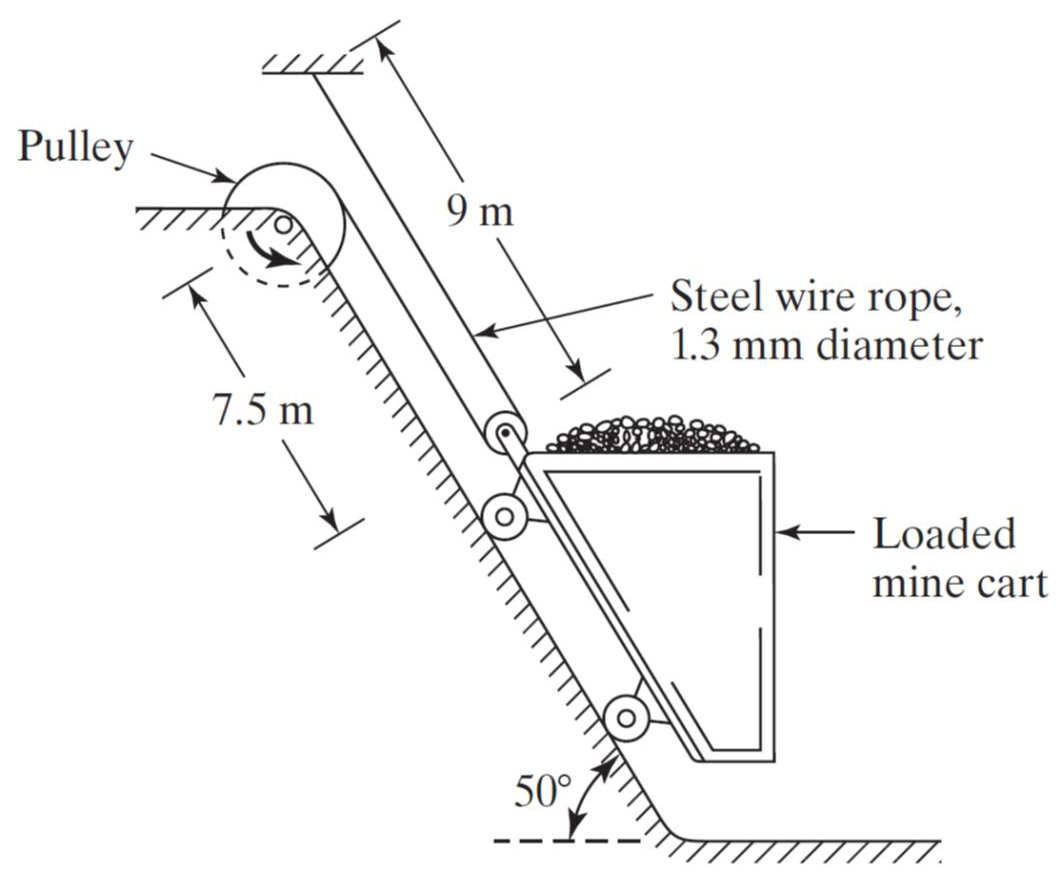
Trouver la fréquence naturelle de vibration du chariot dans la position donnée.
On donne :
$k = \frac{A E}{l}$
Exercice 21 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un châssis électronique de poid 500 N de poids est isolé en le supportant sur quatre ressorts, comme indiqué à la Figure.











Concevoir les ressorts de sorte que l'appareil peut être utilisé dans un environnement dans lequel la fréquence de vibration naturelle varie de 0 à 5 Hz.

Exercice 22 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
Un appareil de commutation électrique est supporté par une grue par un câble en acier de 4 m de long et de 0,01 m de diamètre.
Si la période de vibration axiale naturelle du mécanisme de commutation est de 0,1 s, trouvez la masse du mécanisme de commutation.



















Exercice 23 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
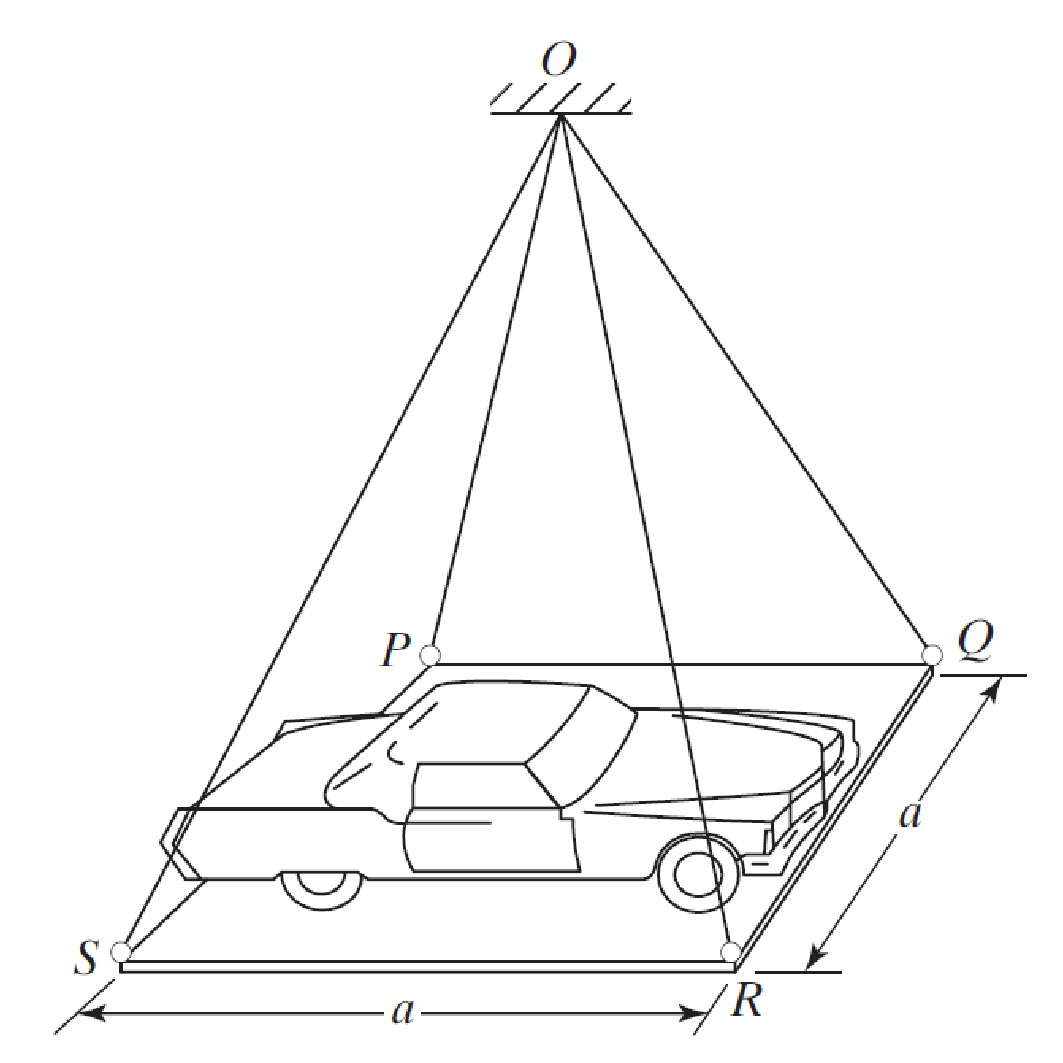
La plate-forme carrée (P Q R S) et la voiture de la figure ont une masse combinée M.
La plateforme est suspendue par quatre fils élastiques à un point fixe O, comme indiqué sur la figure. La distance verticale entre le point de suspension O et la position d'équilibre horizontal de la plate-forme est h.
Si le côté de la plateforme est "a" et que la rigidité de chaque fil est égale à "k", déterminer la période naturelle des vibrations verticales de la plate-forme.
On donne : $\sqrt{1+F}=1+\frac{{\displaystyle F}}{{\displaystyle 2}}$









Exercice 24 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
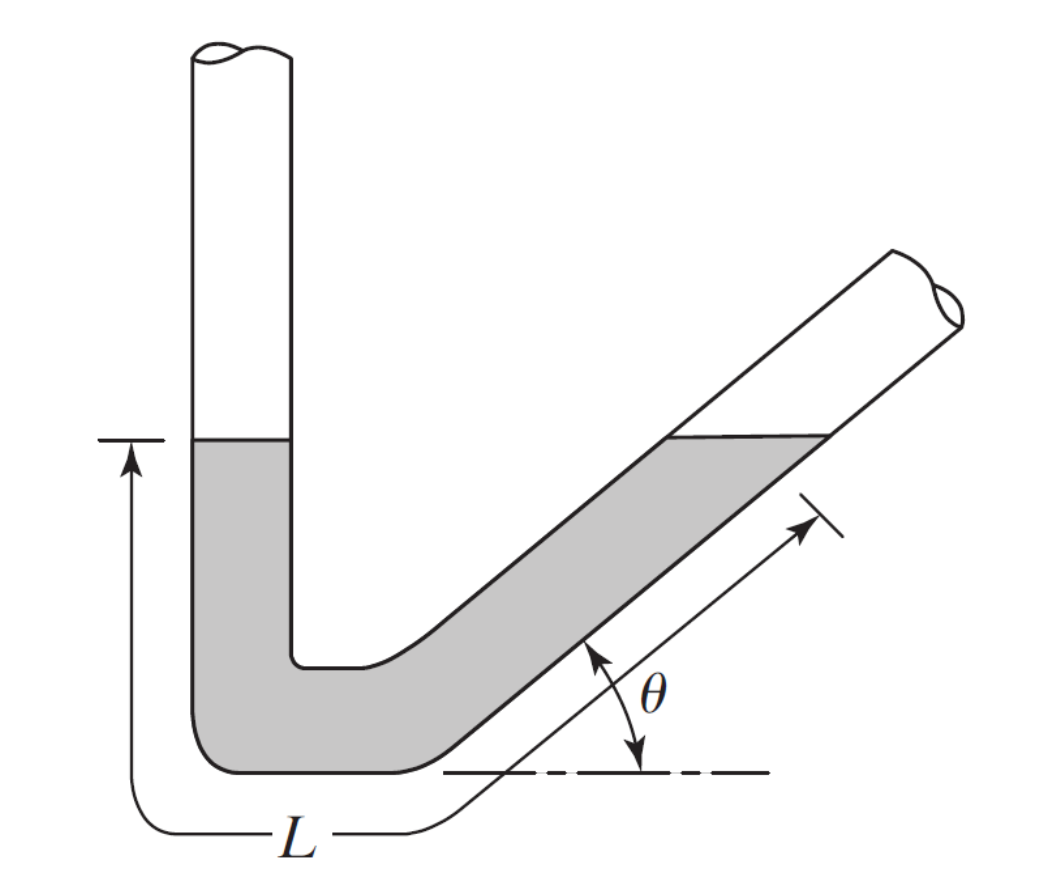
Le manomètre incliné, illustré à la figure, est utilisé pour mesurer la pression. Si la longueur totale du mercure dans le tube est L, trouvez une expression pour la fréquence naturelle des oscillations du mercure.
On donne : $dm = A \rho dx$









Exercice 25 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
La caisse, de masse de 250 kg, suspendue à un hélicoptère (voir Figure(a)) peut être modélisée comme indiqué à la Figure (b).
Les pales du rotor de l'hélicoptère tournent à 300 tr / min.


















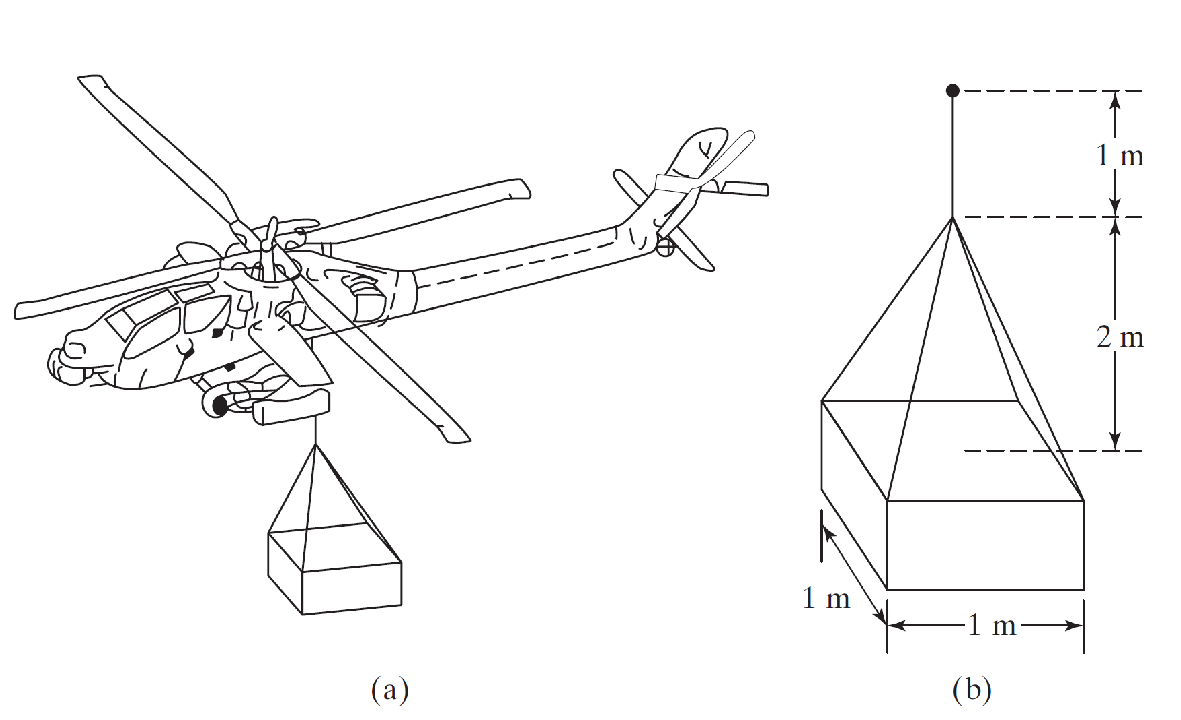
Trouver le diamètre des câbles en acier de telle sorte que la fréquence de vibration naturelle de la caisse soit au moins deux fois supérieure à celle des pales du rotor.
On donne :$E=207\times \hspace{0.17em}{10}^9 et k=\frac{A\hspace{0.17em}E}{\ell }$

Exercice 26 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
La figure montre un engin spatial avec quatre panneaux solaires.
Chaque panneau a les dimensions $1.5 m \times 1 m \times 0.025 m$ avec une densité de poids de 2690 $kg /m^ 3 $ et est relié au corps de l’engin spatial par des tiges en aluminium de 0.3 m de longueur et de 25 mm de diamètre.













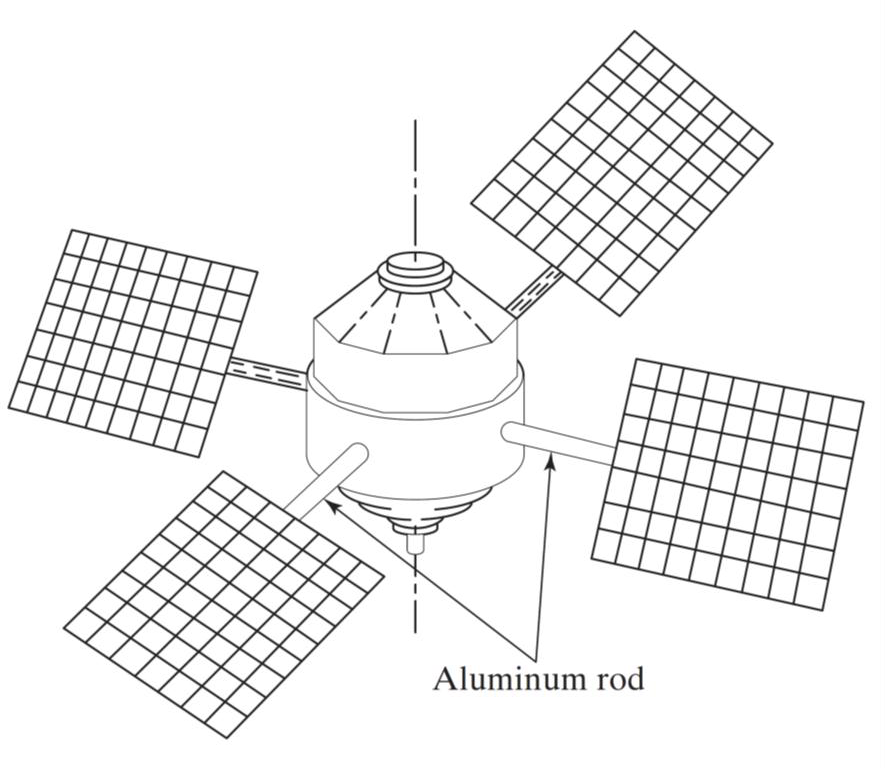
En supposant que le corps de l’engin spatial soit très grand (rigide), déterminer la fréquence naturelle de vibration de chaque panneau autour de l’axe de la tige de connexion en aluminium.
Le moment d'inertie du panneau par rapport à $x$ est donnée par: $J=\frac{m}{12}\left(a^2+b^2\right)$
On donne : $k=\frac{G\hspace{0.17em}{I}_0}{\ell }$
Avec $G= 2.6 {10}^{10}$ pa est le Module de cisaillement de l'aluminium
$I_0=\frac{\pi }{32}\hspace{0.17em}{d}^4$ est le moment polaire de la section de la tige

Exercice 27 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
supporté par un ensemble de câbles d'acier d'une longueur de 2 m comme représenté sur la figure. La durée de vibration axiale (dans le sens vertical) varie de 5 à 4,0825 s, lorsque une masse supplémentaire de 5 000 kg étant ajoutée à la tête du récipient sous pression.
Déterminer la section équivalente des câbles et la masse de la tête du récipient sous pression.
On donne : $k=\frac{A\hspace{0.17em}E}{\ell }$














Exercice 28 (Ajouté le 4 novembre 2019 - أضيف يوم 04 /11 /2019 )
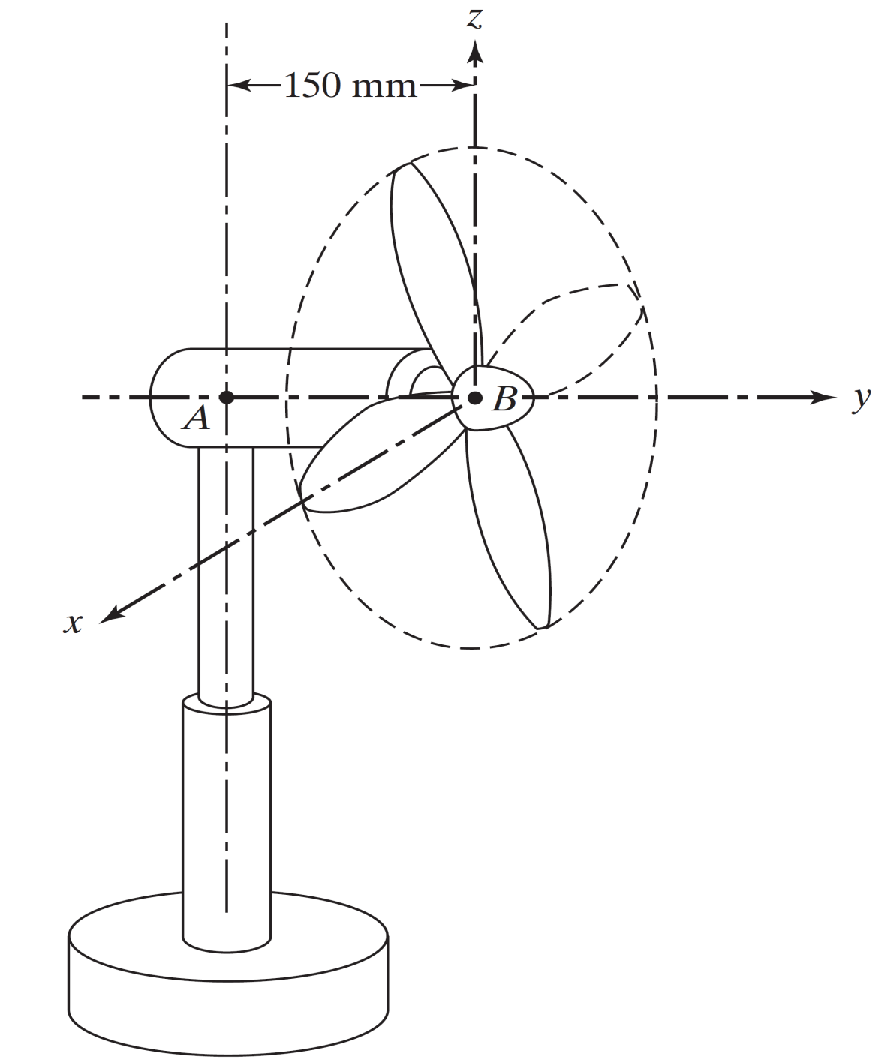
Une des pales d'un ventilateur électrique est retirée (comme indiqué en pointillés sur la figure).
L'arbre en acier AB, sur lequel les lames sont montées, équivaut à un arbre uniforme de 25 mm de diamètre et de 150 mm de longueur. Chaque lame peut être modélisée comme une tige mince uniforme de 2 Kg et de 300 mm de longueur.
Déterminer la fréquence naturelle de vibration des trois pales restantes autour de l'axe des ordonnées.
On donne : $k=\frac{{\displaystyle G I_0}}{{\displaystyle {\ell }_{AB}}}$ , $I_0=\frac{{\displaystyle \pi }}{{\displaystyle 32}} d^4$, avec : G= 87 $\times {10}^9$