Exercice 1.
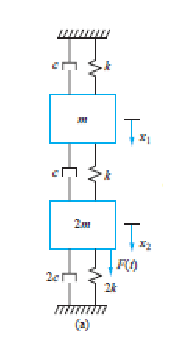
Établir les équations différentielles régissant le mouvement du système à deux degrés de liberté de la figure 5.6 en utilisant x1 et x2 comme coordonnées généralisées. Les deux sont mesurés à partir de position d'équilibre du système.






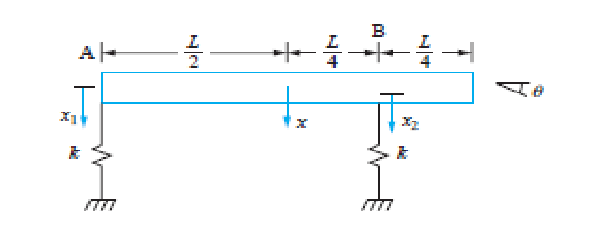
Exercice 2
Prenons le système illustré à la figure 5.7, dans lequel la tige de masse m et de moment d’inertie $m\hspace{0.17em}{L}^2/12$ est attachée à des ressorts de raideur k aux point A et B.
Établir les équations différentielles pour le système de la figure en utilisant x en coordonnées généralisées: le déplacement du centre de masse du bar par rapport à l'équilibre et $\theta$ correspond au déplacement angulaire dans le sens des aiguilles d'une montre.
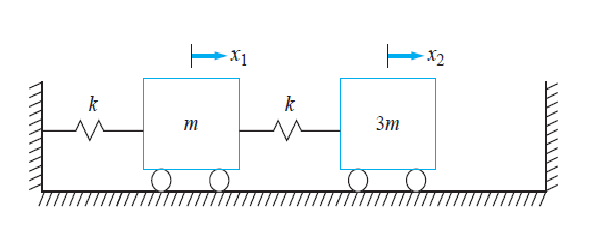
Exercice 3
Considérons le système à deux degrés de liberté illustré à la figure 6.8. Déterminez
(a) les fréquences propres
(b) les modes
(c) les nœuds du système

Exercice 4
Pour le système de l'exercice 2 calculer les fréquences propres et les modes propres.
Exercice 5
Pour le système de l'exercice 3 on donne les déplacements initiaux de $x_1\left(0\right)=\delta$ et $x_2\left(0\right)=-\delta$ et est libéré du repos. Déterminez la réponse résultante du système.


Exercice 6
Déterminez les équations différentielles du mouvement pour le système de la figure 5.10



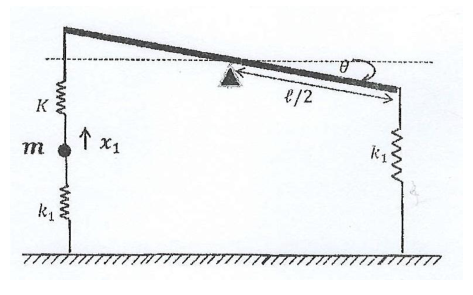
Exercice 7
une barre de longueur l et de masse M reposant en son milieu sur un pivot fixe est couplée à une masse ponctuelle m par l'intermédiaire d'un ressort de raideur K (voir figure 5.11). La masse et la barre sont reliées à un bâti fixe à l'aide de deux ressorts de même raideur $k_1$. A l'équilibre, la barre est horizontale et les ressorts sont non déformés.
1. Établir les équations différentielles du mouvement de vibrations de faible amplitude. On posera : $x_2=l\hspace{0.17em}\theta /2$, M=9 m et $K=k_1$.
2. Déterminer les pulsations propres du système ${\omega }_{01}$ et ${\omega }_{02}$ en fonction de $\Omega =\sqrt{k_1/m}$
3. Calculer le rapport d'amplitudes dans le deuxième mode de vibration. En déduire les solutions $x_1\left(t\right)$ et $x_2\left(t\right)$ dans ce même mode.
Exercice 8
Soit le montage de la figure 5.12. Les 2 cylindres identiques (masse M, rayon R, et moment d’inertie ($J=\frac{M{R}^2}{2}$) roulent sans glisser sur un support horizontal. Soit ${\theta }_1$ et ${\theta }_2$ les angles de rotation de ces 2 cylindres par rapport à leurs positions d'équilibre respectives. Au repos (${\theta }_1$ = ${\theta }_2$ = 0) les ressorts sont non déformés.
1. On prend $k_1=k_2=k’\ne k$, trouver les équations du mouvement en fonction de $x_1$ et $x_2$.
2. En déduire les pulsations propres.
3. Déterminer le coefficient de couplage.

Exercices de Vibrations / Chapitre 6 : Vibrations forcées à 2 ddL

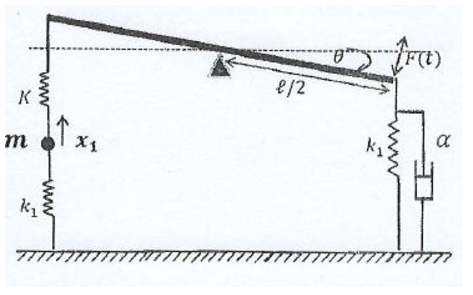
Exercice 1
On étudie le système de la barre couplée à la masse ponctuelle, en régime forcé en tenant compte de l'amortissement. La force sinusoïdale $F\left(t\right):F_0\hspace{0.17em}\cos \omega \hspace{0.17em}t$, est appliquée perpendiculairement à l'extrémité de barre (voir figure) avec : M=9 m et $K=k_1$
1. Établir les équations différentielles du mouvement pour les coordonnées $x_1$ et $x_2$, où $x_2=l\hspace{0.17em}\theta /2$. En déduire les réponses $x_1\left(t\right)$ et $x_2\left(t\right)$ en régime permanent.
2. Quelle pulsation \omega faut-il choisir pour arrêter le mouvement de la barre. En déduire l'amplitude $X_1$ de vibration de la masse m.
3. Dans le cas où l'amortissement est négligé, déterminer la (les) pulsations de résonances.

Exercice 2
Dans le système oscillant représenté sur la Figure 6.4, le cylindre est homogène, de masse M et de rayon R. Ce cylindre est relié au point A par un ressort de coefficient de raideur K à un bâti B1 animé d'un mouvement sinusoidale d'amplitudes S0 et de pulsation $\omega$. Il est également relié par un amortissement de coefficient c à un bâti fixe B2. Le cylindre roule sans glisser sur un plan horizontal. La tige est sans masse et de longueur l.
L'une de ses extrémités peut osciller sans frotement autour de l'axe du cylindre. Elle porte à l'autre extrimité une masse ponctuelle m qui est reliée à un bâti fixe B_3 par un ressort coefficient de raideur k.
A l'équilibre la tige est verticale et l'axe du cylindre G est est à l'origine des coordonnées O, on suppose aussi que les ressorts ne sont pas déformés.
La rotation de la tige par rapport à la vertical est repérée par l'angle $\phi$ et celle du cylindre par l'angle $\theta$. On considère les oscillations de faibles amplitudes.
On pose :
3M=2m, 4K=k=m g/l, $x_2=l\hspace{0.17em}\phi$ $x_1=R\hspace{0.17em}\theta$.
1. Déterminer les équations différentielles en $x_1\left(t\right)$ et $x_2\left(t\right)$. Montrer que le système est équivalent à un système forcé soumis à une force F(t) sinusoïdale dont on précisera l'amplitude F0.
2. Déterminer l'impédance d'entrée du système à la pulsation $\omega =\Omega =\sqrt{\frac{k}{m}}$. Exercice 3
Soit le système mécanique représenté sur la figure 6.5. La masse mz est soumise à une force $F\left(t\right)=F_0 \cos \omega \hspace{0.17em}t$.
1. Écrire les équations différentielles, en x1(t) et x2(t), qui régissent les déplacements horizontaux des masses m1 et m2 lors de petites oscillations.
2. Réécrire les équations du mouvement dans leurs formes intégro-différentielles.
3. Déduire l'impédance d'entrée du système $Z_e=\frac{F\left(t\right)}{{\dot{x}}_2}$.