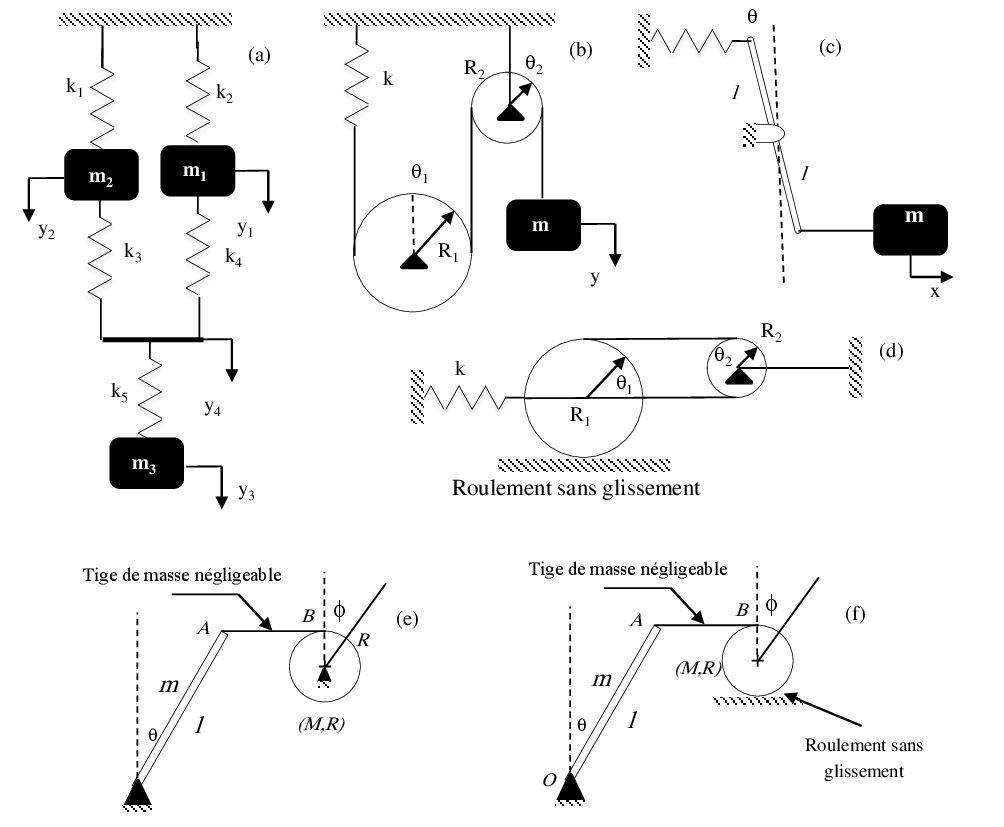
Exercice 1 Déterminer le degré de liberté de chaque système.
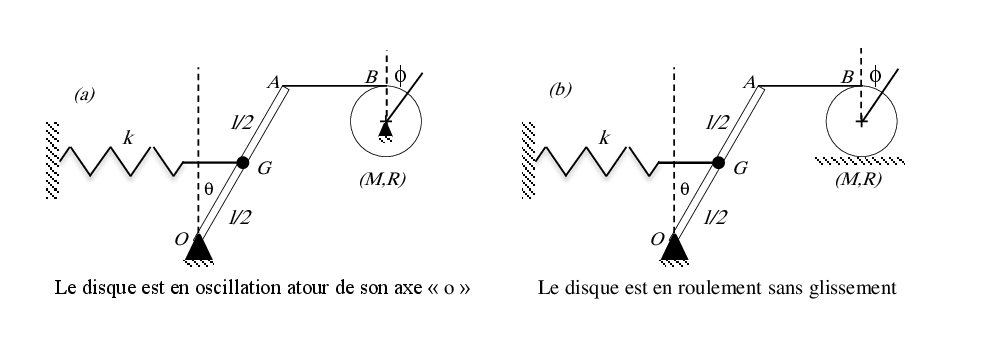
Exercice 2 Déterminer l’énergie cinétique et l’énergie potentielle pour chaque système.
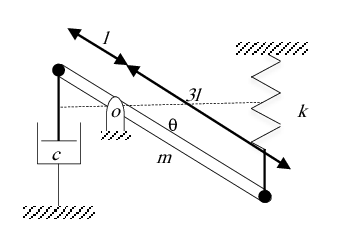
Exercice 3 Soit le système mécanique composé d’une barre AB (m, 4 l) qui peut osciller autour d’un axe o, d’un ressort k et d’un amortisseur c.
1. Pour des faibles oscillations $(\sin \theta = \theta)$,déterminer l'énergie cinétique, l'énergie potentielle et la fonction de dissipation.
2. Déduire la nature du mouvement oscillatoire.
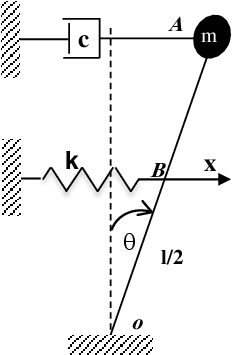
Exercice 4 Soit le système suivant. On considère que Pour des petites oscillations et que la tige est de masse négligeable et de longueur l.
1. Calculer l’énergie cinétique du système.
2. Etablir l’équation différentielle du mouvement et donner la nature du mouvement oscillatoire.
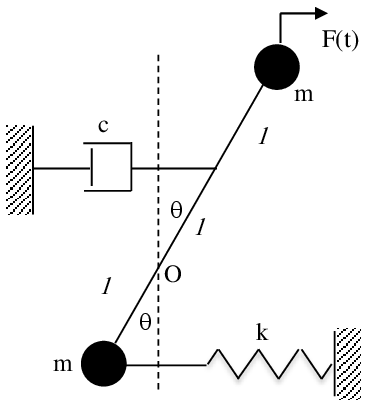
Exercice 5 Le système de la figure, est forcé à osciller autour de la verticale, qui est la position d'équilibre, par une force sinusoïdale F qui reste horizontale lors du mouvement.
Elle est donnée par . Les frottements sont modélisés par un frottement visqueux de coefficient c. On suppose que l’amplitude du mouvement reste faible pour admettre l’approximation des faibles angles.
1. Établir l’équation différentielle du mouvement.
