Soit un transformateur parfait 380 V/220 V , 50 Hz, de puissance apparente nominale S=2 kVA.
1. Calculer les courants nominaux I1N, I2N et le rapport de transformation m.
2. La charge inductive est constituée d’une résistance R=20 Ω en série avec une inductance L=50 mH. Calculer l’impédance de la charge et son facteur de puissance.
3. En déduire les courants du transformateur et la puissance active fournie.
Exercice 2
La puissance apparente d’un transformateur monophasé 5 kV / 230 V ; 50 Hz est S = 21 kVA. La section du circuit magnétique est s = 60 cm2 et la valeur maximale du champ magnétique B = 1,1T.
. - L’essai à vide a donné les résultats suivants : U1 = 5 000 V ; U20 = 230 V ; I10 = 0,50 A et P10 = 250 W.
- L’essai en court-circuit avec I2CC = I2n a donné les résultats suivants : P1CC = 300 W et U1CC = 200 V. 1. Calculer le nombre de spires N1 au primaire.
2. Calculer le rapport de transformation m et le nombre N2 de spires au secondaire.
3. Quel est le facteur de puissance à vide de ce transformateur ?
4. Quelle est l’intensité efficace du courant secondaire I2N ?
5. Déterminer les éléments RS ; ZS et XS de ce transformateur.
6. Calculer le rendement de ce transformateur lorsqu’il débite un courant d’intensité nominale dans une charge inductive de facteur de puissance 0,83.
Exercice 3
L’étude d’un transformateur monophasé a donné les résultats suivants :
- Mesure en continu des résistances des enroulements à la température de fonctionnement : r1 = 0,2 Ω et r2 = 0,007 Ω.
- Essai à vide : U1 = U1N = 2 300 V ; U20 = 240 V ; I10 = 1,0 A et P10 = 275 W.
- Essai en court-circuit : U1CC = 40 V ; I2CC = 200 A.
1. Calculer le rapport de transformation m.
2. Montrer que dans l’essai à vide les pertes Joule sont négligeables.
3. Déterminer la valeur de la résistance ramenée au secondaire RS.
4. Calculer la valeur de P1CC.
5. Déterminer XS.
6. Déterminer par la méthode de votre choix, la tension aux bornes du secondaire lorsqu’il débite un courant d’intensité I2 = 180 A dans une charge capacitive de facteur de puissance 0,9.
7. Quel est alors le rendement.
Exercice 4
Les essais d’un transformateur monophasé ont donné les résultats suivants :
- Essai à vide sous tension primaire nominale : U1n = 2,20 kV ; f = 50 Hz ; Valeur efficace de l’intensité du courant mesuré au primaire : U20 = 230 V ; Puissance active mesurée au primaire : P10 = 700 W ;
- Essai en court-circuit sous tension primaire réduite : U1cc = 130 V ; I2cc = 200A et P1cc = 1,50 kW.
1. Proposer un schéma de câblage du transformateur permettant lors de l’essai à vide, avec tous les appareils pour mesurer I10, U20, P10 en indiquant le type d’appareil choisi.
2. Calculer le rapport de transformation m.
3. Calculer le facteur de puissance du transformateur lors de l’essai à vide
4. On note I10r la valeur efficace de la composante réactive de l’intensité I10. Calculer I10r (appelé parfois courant magnétisant).
5. On appelle RS la résistance des enroulements ramenés au secondaire et XS la réactance ramené au secondaire.
a- Proposer un schéma de câblage du transformateur lors de l’essai en court-circuit, avec tous les appareils permettant de mesurer U1cc, I1cc, P1cc. b- Pourquoi cet essai est-il réalisé sous tension primaire réduite ?
c- Faire un schéma électrique équivalent du transformateur ramené au secondaire pour cet essai ; y porter toutes les grandeurs électriques. d- Que représente la puissance active P1cc lors de cet essai ?
e- Calculer RS.
f- Calculer le module de l’impédance ZS ramené au secondaire. Déduire XS
6. Le secondaire alimente maintenant une charge inductive de facteur de puissance 0,8. U1n = 2,2 kV. On relève I2n = 200A.
a- Faire un schéma électrique équivalent du montage, le transformateur étant représenté par son modèle ramené au secondaire. b- Calculer une valeur approchée de U2.
c- En déduire la puissance active fournie à la charge.
d- Quel est la valeur des pertes dans le fer Pf ? … des pertes Joules Pj ? et calculer la puissance active P1.
e- Calculer le rendement du transformateur
Exercice 5
Les essais d’un transformateur monophasé ont donné :
- A vide : U1 = 220V, 50 Hz (tension nominale du primaire) ; U20 = 44V ; P10 = 80W et I10 = 1A.
- En continu au primaire : U1 = 5V ; I1 = 10A.
- En court-circuit : U1cc = 40V ; P1CC = 250W ; I1CC = 20A (courant nominale primaire).
1.1 Déterminer le rapport de transformation, et le nombre de spires du secondaire si l’on en compte 520 au primaire.
1.2. Vérifier que l’on peut négliger les pertes par effet Joule lors de l’essai à vide. En admettant que les pertes fer sont proportionnelles au carré de la tension primaire, montrer qu’elles sont négligeables dans l’essai en court-circuit.
1.3. Déterminer les valeurs de Xs et RS.
2. Le transformateur, alimenté au primaire sous sa tension nominale, débite 100A au secondaire avec un facteur de puissance égal à 0,9 (charge inductive).
2.1. Déterminer graphiquement la tension secondaire du transformateur. En déduire la puissance délivrée au secondaire.
2.2. Déterminer la puissance absorbée au primaire, ainsi que le facteur de puissance.
Exercice 6
L’étude d’un transformateur monophasé 1500V, 225V, 50 Hz de puissance apparente 44 kVA, a donné les essais suivants :
- Essai en continu au primaire : U1 = 2,5V ; I1 = 10A ;
- Essai à vide : U1 = 1500V ; I10 = 2A ; U20 = 225 V ; P10 = 300W ;
- Essai en court-circuit : U1cc = 22,5V ; I1cc = 22,5 A ; P1cc = 225W.
1. Déterminer le rapport de transformation
2.a. Calculer la composante active du courant lors de l’essai à vide
2.b. Vérifier que l’on peut négliger les pertes par effet Joule lors de l’essai à vide :
2.c. Montrer que les pertes fer sont négligeables dans l’essai en court-circuit, en admettant qu’elles sont proportionnelles au carré de la tension primaire. Calculer les éléments RS et XS des enroulements ramenés au secondaires.
3. Le transformateur alimenté au primaire sous une tension U1 = 1500 V débite un courant constant d’intensité I2 = 200A, quel que soit la charge.
3. a. Déterminer la valeur de déphasage entre courant et tension secondaire, pour que la chute de tension soit nulle.
3. b. Déterminer la chute de tension relative pour facteur de puissance de 0,8.
4. Déterminer le rendement .
Exercice 7
Un transformateur de distribution possède les caractéristiques nominales suivantes : S2N = 25 kVA, PJ= 700 W et Pfer = 115 W.
1. Calculer le rendement nominal pour :
- une charge résistive
- une charge inductive de facteur de puissance 0,8
Exercice 8
Un transformateur monophasé a les caractéristiques suivantes :
- tension primaire nominale : U1N = 5375 V / 50 Hz
- rapport du nombre de spires : N2/N1 = 0,044
- résistance de l’enroulement primaire : R1 = 12 Ω
- résistance de l’enroulement secondaire : R2 = 25 mΩ
- inductance de fuite du primaire : L1 = 50 mH
- inductance de fuite du secondaire : L2 = 100 μH
1. Calculer la tension à vide au secondaire.
2. Calculer la résistance des enroulements ramenée au secondaire RS.
3- Calculer l’inductance de fuite ramenée au secondaire LS. En déduire la réactance de fuite XS.
Le transformateur débite dans une charge résistive R = 1Ω
4. Calculer la tension aux bornes du secondaire U2 et le courant I2qui circule dans la charge.
Exercice 9
Un grand transformateur fonctionnant à vide prélève un courant d'excitation I1o de 5 A lorsque le primaire est connecté à une source de 120 V, 60 Hz. Un test de wattmètre a montré que les pertes fer sont égal à 180 W.
Calculer
1. La puissance réactive absorbée par le noyau
2. La valeur de R0 et X0
3. La valeur de I10a, I10r et I10
Exercice 10
L'enroulement secondaire d'un transformateur possède 180 tours. Lorsque le transformateur est sous charge, le courant secondaire a une valeur efficace de 18 A, 60 Hz. De plus, le flux mutuel Φm a une valeur maximale de 20 mWb. Le flux de fuite secondaire Φf2 a une valeur maximale de 3 mWb.
Calculer
1. La tension induite dans l’enroulement secondaire par son flux de fuite
2. La valeur de la réactance de fuite secondaire
3. La valeur de V2 induite par le flux mutuel Φm
Exercice 11
La plaque signalétique d’un transformateur de distribution indique 250 kVA, 60 Hz, primaire 4160 V, secondaire 480 V.
1. Calculer les courants nominaux primaire et secondaire
2. Si on applique 2000 V au primaire de 4160 V, pouvons-nous toujours tirer 250 kVA du transformateur?
Exercice 12
Un transformateur monophasé de 3000 kVA, 69 kV / 4,16 kV, 60 Hz a une impédance interne totale Zp de 127, côté primaire.
Calculer
1. Les courants nominaux primaire et secondaire
2. Régulation de tension de vide à plein pour une charge résistive de 2000 kW, sachant que la tension d'alimentation primaire est fixée à 69 kV
3. Les courants primaire et secondaire si le secondaire est accidentellement court-circuité
Exercice 13
Lors d'un test en court-circuit sur un transformateur de 500 kVA, 69 kV / 4,16 kV, 60 Hz, les mesures de tension, de courant et de puissance suivantes ont été effectuées. Les bornes X1, X2 étaient en court-circuit (voir Figure):
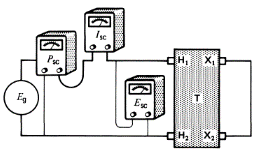
Calculer
1. L'impédance du transformateur référée au primaire
2. La résistance référée au primaire
3. La réactance de fuite référée au primaire
Exercice 14
Un test de circuit ouvert a été réalisé sur le transformateur donné dans l’exercice 13. Les résultats suivants ont été obtenus lorsque l'enroulement BT était excité. (Dans certains cas, comme dans un atelier de réparation, une tension de 69 kV peut ne pas être disponible . Ce test doit être effectué en excitant l’enroulement BT à sa tension nominale.)
En utilisant ces informations et les caractéristiques du transformateur trouvées dans l’exercice 13, Calculer les valeurs de X0 et R0 du côté primaire
Exercice 15
Un transformateur de 100 kVA est connecté en parallèle avec un transformateur existant de 250 kVA pour alimenter une charge de 330 kVA. Les transformateurs ont une tension nominale de 7 200 V / 240 V, mais le transformateur de 100 kVA a une impédance de 4%, tandis que le transformateur 250 kVA a une impédance de 6% (Figure).
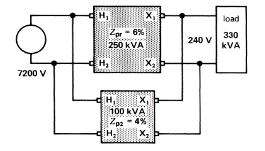
Calculer
1. Le courant primaire nominal de chaque transformateur
2. L'impédance de la charge référée au côté primaire
3. L'impédance de chaque transformateur référée au côté primaire
4. Le courant primaire réel dans chaque transformateur


