Exercice 1
Une machine synchrone triphasée, à 6 pôles par phase, est prévue pour fonctionner sur un réseau : 220/380V ;50Hz. Un essai à vide à 50Hz de cette machine a donné les valeurs suivantes :

Iex	0	5	10	15	20	25	30	35	40	45	50	60
E0 composée	0	136	262	349	411	465	504	534	563	588	611	650

Le stator est couplé en étoile, La résistance du stator a été mesurée entre deux bornes du stator et a donnéR_m=1.4 Ω. Un essai en dédit réactif a donné Iex=35 A, I=20 A, u=291 V.
1. A quelle vitesse, doit –on entrainer cette machine pour que la fréquence soit de 50 Hz.
2. Déterminer la résistance R et la réactance synchrone XS.
Exercice 2
Pour un alternateur triphasé, on a mesuré le courant dans la ligne I et la tension composée U (entre 2 bornes), Déterminer :
1. La résistance équivalente Rm entre les bornes de l’alternateur.
2. Les pertes par effet Joules dans l’enroulement statorique en fonction de I et U (étudier le cas où l’enroulement statorique est couple en étoile, puis en triangle).
Exercice 3
L’induit d’un alternateur triphasé étoile, dont la fréquence est 50 Hz et la vitesse nominale de rotation 500 tr/min, a 72 encoches et l’on sait que chaque encoche comporte 12 conducteurs.
Sachant que l’induction dans l’entrefer est 0.6 tesla, et la surface des pièces polaires est 640 cm2 , on demande :
1- Le nombre de pôles de l’alternateur.
2- Sa F.E.M.
Exercice 4
Une turbine hydraulique tournant à 200 tr / min est reliée à un générateur synchrone. Si la tension induite a une fréquence de 60 Hz, combien de pôles le rotor a-t-il? :
Exercice 5
Un générateur synchrone triphasé produit une tension de ligne à circuit ouvert de 6928 V lorsque le courant d'excitation continu est de 50 A. Les bornes alternatives sont ensuite court-circuitées et les courants de ligne sont de 800 A.
a) Calculez la réactance synchrone par phase.
b) Calculez la tension aux bornes si trois résistances de 12 Ω sont connectées en étoile aux bornes.


Exercice 6
Un alternateur triphasé de 36 MVA, 20,8 kV a une réactance synchrone de 9 Ω et un courant nominal de 1 kA. La courbe de saturation à vide donnant la relation entre Eo et Ix est donnée à la Figure.























Si l'excitation est réglée de manière à ce que la tension aux bornes reste fixée à 21 kV, calculer le courant d'excitation nécessaire et tracez le diagramme de phaseur dans les conditions suivantes:
a) Sans charge
b) Charge résistive de 36 MW
c) Charge capacitive de 12 Mvar

Exercice 7
Un générateur triphasé possède une réactance synchrone de 6 et la tension d'excitation Eo est de 3 kV par phase.
Calculer la tension ligne à neutre V pour une charge résistive de 8 Ohm et tracer le diagramme de Fresnel.
Exercice 8
Un générateur triphasé de 3000 KVA, 20 kV, 900 tr / min, 60 Hz fournit de l'énergie à une charge de 2400 KVA, 16 kV, avec un facteur de puissance 0,8 inductif.
Si la réactance synchrone est de 100 Ω, calculer la valeur de Eo, par phase. Considérer le courant comme référence de phase
Exercice 9
OUn générateur triphasé, 500 MVA, 0,95 facteur de puissance, 15 kV, 60 Hz, 200 tr / min. Ce générateur synchrone a une efficacité de 98,4% lorsqu'il délivre une puissance de 500 MW. Sachant que le courant d'excitation continu est de 2400 A à une tension continue de 300 V, calculer ce qui suit:
1- Les pertes totales dans la machine
2- Les pertes de cuivre dans le rotor
3- Le couple développé par la turbine

Exercice 10
En vous référant à la figure, chaque bobine du rotor a 21,5 tours et porte un courant continu de 500 A. Sachant que la longueur de l'entrefer est de 1,3 pouces, calculer la densité de flux dans l'entrefer à vide. On Néglige le mmf requis pour la partie fer du circuit magnétique.

Exercice 11
En référence à la figure, les informations suivantes sont données sur un générateur:
E0=12 kV; V=14 kV; Xs=2 Ohms; E0 est en avance de V par δ=30°








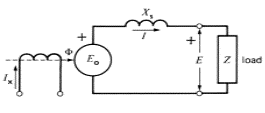
a. Calculer la puissance active totale à la sortie du générateur.
b. Tracer le diagramme de phase pour une phase.
c. Calculer le facteur de puissance de la charge.

Exercice 12
Un alternateur de secours à entraînement par moteur de 33,8 kVA, 480 V, triphasé, 60 Hz est conçu pour fonctionner avec un facteur de puissance de 80% et un rendement de 83,4%.
Calculer la puissance nominale minimale du moteur diesel pour entraîner le générateur

Exercice 13
Un générateur synchrone à turbine à eau de 220 MVA, 500 tr / min, 13,8 kV, 50 Hz, facteur de puissance 0,9, fabriqué par Siemens, présente les propriétés suivantes:
- Classe d'isolation: F
- Moment d'inertie: 525 t m2
- Masse totale du stator: 158 t (t = tonne métrique)
- masse totale du rotor: 270 t
- Efficacité à pleine charge, facteur de puissance unitaire: 98,95%
- Réactance synchrone non saturée: 1,27 pu
- réactance transitoire: 0,37 pu
- Vitesse de fuite en mode générateur: 890 tr / min
- On utilise une excitation statique et le courant d'excitation est de 2980 A sous une tension d'excitation de 258 V.

Le générateur est également conçu pour fonctionner comme un moteur, entraînant la turbine comme une pompe. Dans ces conditions, le moteur développe une puissance de 145 MW.

Le stator et le rotor sont refroidis à l'eau en faisant passer l'eau à travers les conducteurs creux. L'eau est traitée de manière à ce que sa conductivité soit inférieure à 5 μS / cm. L'eau pure circule dans le stator à un débit de 8,9 litres par seconde et à travers le rotor à 5,9 litres par seconde. Compte tenu des informations ci-dessus, effectuer les calculs suivants:

a. La puissance de sortie nominale, en MW à facteur de puissance unitaire et à facteur de puissance retardé de 0,9
b. La puissance de sortie réactive nominale, en Mvar
c. Le rapport de court-circuit
d. La valeur de la réactance synchrone ligne à neutre, par phase
e. Les pertes totales du générateur à pleine charge pour un facteur de puissance unitaire

Exercice 14
Un moteur synchrone de 500 ch, 720 tr / min, connecté à une ligne triphasée de 3980 V, génère une tension d'excitation Eo de 1790 V (ligne à neutre) lorsque le courant d'excitation continu est de 25 A. La réactance synchrone est de 22 Ω et l'angle entre Eo et V est de 30 °.
Calculer
a. La valeur de Ex
b. Le courant alternatif
c. Le facteur de puissance du moteur
d. La puissance approximative développée par le moteur
e. Le couple approximatif développé à l'arbre

Exercice 15
Un moteur synchrone de 4000 ch (3000 kW), 6600 V, 60 Hz, 200 tr / min fonctionne à pleine charge avec un facteur de puissance maximal de 0,8. Si la réactance synchrone est de 11 Ω, calculer ce qui suit:
a. La puissance apparente du moteur, par phase
b. Le courant alternatif
c. La valeur et la phase de Eo
d. tracer le diagramme de phaseur
e. Déterminer l'angle de déphasage entre E0 et V

Exercice 16
Un moteur synchrone de 1500 kW, 4600 V, 600 tr / min et 60 Hz possède une réactance synchrone de 16 Ω et une résistance statorique de 0,2 Ω, par phase. La tension d'excitation Eo est de 2400 V et le moment d'inertie du moteur et de sa charge est de 275 kg m2. Nous souhaitons arrêter le moteur en court-circuitant l'induit tout en maintenant le courant du rotor en courant continu.
Calculer
a. La puissance dissipée dans l'induit à 600 tr / min
b. La puissance dissipée dans l'induit à 150 tr / min
c. L'énergie cinétique à 600 tr / min
d. L'énergie cinétique à 150 tr / min
e. Le temps nécessaire pour que la vitesse passe de 600 à 150 tr / min

Exercice 17
Un moteur synchrone triphasé à 225 tr / min, connecté à une ligne de 4 kV à 60 Hz, consomme un courant de 320 A et absorbe 2 000 kW.
Calculer
a. La puissance apparente fournie au moteur
b. Le facteur de puissance
c. La puissance réactive absorbée
d. Le nombre de pôles sur le rotor

Exercice 18
Soit un moteur synchrone dont les paramètres par phase suivants sont donnés :
V=E=2.4 kV; E0=3 kV; Xs=2 Ohms; I=900 A
Tracer le diagramme de phaseur et déterminer:
a. L’angle de déphasage
b. Puissance active, par phase
c. Facteur de puissance du moteur
d. Puissance réactive absorbée (ou délivrée), par phase

Exercice 19
Un moteur synchrone de 6.9 kV de 4 000 hp possède une réactance synchrone de 10 Ω, par phase. Le stator est connecté en étoile et le moteur fonctionne à pleine charge (4000 ch) avec un facteur de puissance de 0,89. Si l'efficacité est de 97%,
Calculer ce qui suit:
a. La puissance apparente
b. Le courant de ligne
c. La valeur de Eo, par phase
d. La puissance réactive totale fournie au système électrique
e. La puissance maximale approximative que le moteur peut développer