Exercice 1
1. Le moteur d’une grue, à excitation indépendante constante, tourne à une vitesse de rotation de 1500 tr/min lorsqu’il exerce une force de 30 k.N pour soulever une charge à la vitesse (linéaire) V1 = 15m/min ; la résistance de l’induit est de 0, 4 Ω. Ce moteur est associé à un réducteur de vitesse dont les pertes, ajoutés aux pertes mécaniques et magnétiques du moteur font que la puissance utile de l’ensemble est égale à 83 % de la puissance électromagnétique transformée dans la machine. Le moment du couple électromagnétique du moteur est proportionnel à l’intensité du courant qui traverse l’induit : Tem = 1, 35 I.
a) Calculer la puissance utile et le moment du couple électromagnétique.
b) Calculer l’intensité du courant dans l’induit, la force contre-électromotrice et la tension U, appliquée à l’induit.
c) Sachant que la puissance consommée par l’excitation est de Pe = 235W calculer la puissance totale absorbée et le rendement du système.
2. En descente la charge, inchangée, entraine le rotor et le machine à courant continu fonctionne alors en génératrice. L’excitation, le rapport du réducteur de vitesse et le rendement mécanique (moteur + réducteur) sont inchangés. On veut limiter la vitesse de descente de la charge à V2 = 12m/min ; calculer :
a) La vitesse angulaire de rotation du rotor.
b) La puissance électromagnétique fournie à la génératrice.
c) Le moment du couple résistant de cette génératrice et l’intensité du courant débité dans la résistance additionnelle.

Exercice 2
Un moteur à courant continu est à excitation indépendante et constante. On néglige sa réaction d’induit. Il a une résistance R = 0, 20 Ω. Il est alimenté sous une tension constante U = 38 V.
1. A charge nominale, l’induit est parcouru par une intensité I = 5 A et il tourne à la vitesse de rotation de 1000 tr/min.
a) Calculer la force électromotrice de l’induit.
b) Calculer le moment du couple électromagnétique Tem.
2. Par suite d’une variation de l’état de charge, l’intensité à travers l’induit devient I’ = 3, 8 A, calculer :
a) Le nouveau moment du couple électromagnétique T’em ,
b) La nouvelle vitesse de rotation Ω’.

Exercice 3
Un moteur shunt est alimenté sous une tension constante de 200 V. Il absorbe un courant It= 22A. La résistance de l’inducteur est r = 100 Ω, celle de l’induit R = 0.5Ω. Les pertes constantes sont de 200 W. Calculer :
a) Les courants d’excitation et d’induit.
b) La force contre électromotrice.
c) Les pertes par effet Joule dans l’inducteur et dans l’induit.
d). la puissance absorbée, la puissance utile et le rendement global.
e)On veut limiter à 30 A l’intensité dans l’induit au d´démarrage. Quel doit être la valeur de la résistance du rhéostat de démarrage.

Exercice 4
Un moteur à excitation série possède une résistance interne totale Rt = 0.1Ω. On suppose que son circuit magnétique n’est pas saturé. Le moteur est utilisé à sa puissance maximale. Alimenté sous une tension Ut= 750 V, il est traversé par un courant d’intensité I= 200 A, la vitesse de rotation de l’arbre vaut alors n= 10 tr/s.
1- Déterminer la force électromotrice du moteur.
2- Calculer le couple électromagnétique.
Le couple utile sur l’arbre n’est alors que de 2100 Nm
3- Calculer le rendement du moteur.
Le moteur est maintenant alimenté sous tension variable. Il entraine une charge qui impose au moteur un couple ´électromagnétique dont le moment est lié à la vitesse de rotation par la relation : Tem = 18 * n2 + 520 , avec Tem en N.m et n en tr/s
4- Vérifier que le moteur est bien capable d’entrainer cette charge, sur toute la gamme de vitesse possible : de 0 à 10 tr/s.
5- Calculer l’intensité du courant, puis la tension à appliquer pour obtenir une vitesse de rotation n0 = 5tr/s.


Exercice 5
Un moteur shunt possède les caractéristiques suivantes :
- Résistance de l’inducteur (sans rhéostat d’excitation) 110 Ω; Résistance de l’induit = 0.2 Ω; Tension d’alimentation = 220V ; Pertes constantes Pc=700W
1-La vitesse de rotation est de 1500 tr/mn quand l’induit absorbe un courant de 75A calculer :
a) représenter le circuit équivalent
b) La force électromotrice
c) La puissance absorbée
d) La puissance utile
e) Le rendement et le couple utile
2-Déterminer la résistance du rhéostat du démarrage pour que l’intensité au démarrage soit de 160A.


Exercice 6
Une machine d’extraction est entrainée par un moteur à courant continu à excitation indépendante. L’inducteur est alimenté par une tension u = 600 V et parcouru par un courant d’excitation d’intensité constante : i = 30 A. L’induit de résistance R = 0.012 est alimenté par une source fournissant une tension U réglable de 0 V à sa valeur nominale : U = 600V. L’intensité I du courant dans l’induit a une valeur nominale :I = 1, 50 kA. La vitesse de rotation nominale est n = 30tr/min.
1) Démarrage
a) Ecrire la relation entre U, E et I , en déduire la tension Ud à appliquer au démarrage pour que Id = 1, 2In.
2) Fonctionnement nominal au cours d’une remontée en charge
a) Exprimer la puissance absorbée par l’induit du moteur et calculer sa valeur numérique.
b) Exprimer la puissance totale absorbée par le moteur et calculer sa valeur numérique.
c) Exprimer la puissance totale perdue par effet Joule et calculer sa valeur numérique.
d) Sachant que les autres pertes valent 27 kW, exprimer et calculer la puissance utile et le rendement du moteur.
e) Exprimer et calculer le moment du couple utile Tu et le moment du couple électromagnétique Tem.

Exercice 7
Une machine à courant continu, pour laquelle on néglige les pertes fer et mécaniques a, une résistance d’induit 0.26 Ω. Les variations de f.é.m. E0 à vide de la machine en fonction de courant inducteur (la vitesse de rotation à vide 1000tr/min) sont décrites par le tableau suivant :

Courant inducteur (A)	0	0.1	0.2	0.3	0.4	0.5	0.7	0.9	1.1	1.5	2
f.e.m E0 à vide	3	12	28	53	85	107	125	134	140	150	155

La réaction magnétique de l’induit est négligeable.
1-Le courant inducteur étant réglé à 1.5 A, la machine fonctionne en moteur en fournissant le couple C1 = 90N.m à une vitesse n1=1500tr/mn. Calculer la tension d’alimentation de l’induit et le courant de l’induit.
2-Un mauvais fonctionnement de l’alimentation de l’inducteur ramène le courant inducteur 0.3A. En supposant que le couple demandé par la charge mécanique ne varie pas, calculer la nouvelle vitesse de rotation du moteur.

Exercice 8
Un générateur à courant continu de force électromotrice 220 V et de résistance interne Rg = 0, 2Ω, débite un courant de 50 A lorsqu’il alimente un réseau composé d’une résistance R connectée en parallèle avec un moteur. Ce dernier, de résistance interne Rm = 0, 2 Ω, absorbe une puissance électrique de Pm= 8400 W.
Calculer :
a) La puissance électrique fournie par le générateur au circuit extérieur.
b) la tension commune entre les bornes du générateur, de la résistance R et du moteur.
c) L’intensité du courant dans le moteur.
d) La force contre-électromotrice du moteur Em.
e)L’intensité du courant dans la résistance R.
f) La valeur de la résistance R.
Exercice 9
On se propose d'étudier un moteur de traction à courant continu à excitation séparée dont les caractéristiques nominales sont : Pu = 165KW ; U=375V; résistance de l’induit R = 0.05 ; résistance de l’inducteur r = 16.
Un essai en moteur alimenté sous sa tension nominale a permis de mesurer un courant induit I=440A et un courant inducteur i=25A pour une vitesse de rotation de  =2000tr/mn. Calculer pour ce fonctionnement :
1- calculer la force électromotrice E. Déduire le couple électromagnétique Tem.
2- Si le rendement est de 0.9, calculer la puissance absorbée. Déduire la tension au stator
3- Calculer les pertes par effet joule au stator et les pertes par effet joule au rotor
4- Calculer la force électromotrice E’ pour une vitesse de ’=3000tr/min. Déduire la nouvelle tension U’ appliquer aux bornes de l’induit pour obtenir cette vitesse.
5- Représenter le circuit équivalent de la machine.
6- La machine fonctionne maintenant en génératrice, l’inducteur est parcouru par le courant i= 25A et l’induit délivre le courant I=300A sous la tension U=375V.Calculer la vitesse de rotation et le couple électromagnétique.
7- Représenter le circuit équivalent de la génératrice.

Exercice 10
Les caractéristiques nominales d’un moteur à excitation indépendante sont : U=100V I=8A; R = 1.25; n=1500tr/min; u = 200V; r = 400
Le flux inducteur est supposé constant
1-Pour le fonctionnement nominal, calculer ; La puissance absorbée par le moteur.
2) Citer une relation donnant la force électromotrice E en fonction de la constante du moteur K, du flux magnétique et de la vitesse de rotation  exprimée en rd/s
3) à partir des données nominales, calculer la force électromotrice nominale
4) L’intensité du courant induit est égale à 8A, le moteur tourne à une vitesse n’=1000tr/mn, déterminer la nouvelle tension U’ à appliquer aux bornes de l’induit
5) Les pertes par effet joule dans l’induit
6) La puissance utile sachant que l’ensemble des pertes collectives valent 80W
7) Le rendement du moteur

Exercice 11
Un tachymètre consiste en une petite machine à courant continu présentant les caractéristiques suivantes: armature à recouvrement, quatre pôles, 780 conducteurs sur l’induit (rotor), champ (stator) par pôle = 0,32 10 -3 Wb.
1- Trouvez l'étalonnage de la vitesse d'un voltmètre à très haute impédance connecté au circuit d'induit.

Exercice 12
Un générateur à courant continu excité séparément présente une courbe de saturation à vide, comme illustré à la figure. 1, et un circuit équivalent, comme indiqué à la figure. 2.

















Les données de la plaque signalétique sont les suivantes: 5 kW, 125 V, 1150 tr / min et la résistance du circuit d’induit 0,40 Ω.
Supposons que le générateur soit entraîné à 1200 tr / min et que le courant soit ajusté par un rhéostat à 2 A.











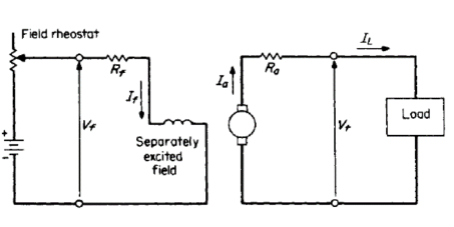
1. Si la charge est celle indiquée sur la plaque signalétique, rechercher la tension aux bornes de l’induit.
Exercice 13
Un générateur continu à enroulement continu présente les données suivantes: 500 kW, 600 V, 4 pôles, 4 interpoles, 464 conducteurs d'induit. La force magnétomotrice (F.M.M) des interpoles est de 20% plus grande que celle de l'armature
1. Déterminer le nombre de tours sur les interpoles.
Exercice 14
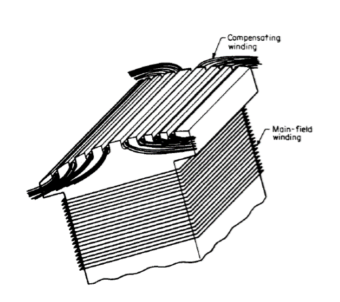
Une machine à courant continu à enroulement a les données suivantes: quatre pôles, rapport de la face des pôles à la portée des pôles = 0,75, nombre total de fentes d'induit = 33, nombre de conducteurs par fente = 12.
1. Concevez un enroulement de compensation pour chaque face de pôle (c.-à-d. Trouver le nombre de conducteurs à placer dans chaque face de pôle et le nombre de fentes sur cette face). Voir la figure suivante.













Exercice 15
L'induit d'un générateur à courant continu à aimant permanent a une résistance de 1 Ω et génère une tension de 50 V lorsque la vitesse est de 500 tr / min. Si l’induit est connectée à une source de 150 V, calculez ce qui suit:
1. Le courant de démarrage.
2. La f.é.m lorsque le moteur tourne à 1000 tr / min et à 1460 tr / min.
3. Le courant d'induit à 1000 tr / min et à 1460 tr / min.
Exercice 16
Un moteur à vitesse variable de 2000 kW, 500 V est entraîné par un générateur de 2500 kW, utilisant le système de contrôle Ward-Leonard illustré à la Figure. La résistance totale du circuit d'induit du moteur et de la génératrice est de 10 ohms. Le moteur tourne à une vitesse nominale de 300 tr / min, lorsque E est égal à 500 V











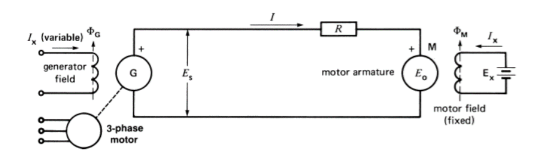
Calculer
1. Le couple moteur et la vitesse lorsque Es = 400 V et E = 380 V.
2. Le couple moteur et la vitesse lorsque Es = 350 V et E = 380 V.
Exercice 17
Un moteur à aimants permanents équipé d'aimants au cobalt-samarium perd 3% de son magnétisme pour une augmentation de température de 100 ° C. Le moteur tourne à une vitesse à vide de 2500 tr / min lorsqu'il est connecté à une source de 150 V à une température ambiante de 22 ° C.
1. Estimer la vitesse si le moteur est placé dans une pièce où la température ambiante est de 40 ° C.
Exercice 18
Une machine à courant continu à quatre pôles a un enroulement en vague de 300 tours. Le flux par pôle est 0: 025 Wb. La machine à courant continu tourne à 1000 tr / min.
1. Déterminer la tension générée.
2. Déterminer la puissance électromagnétique en kW si le courant nominal de 50 A.