Exercice 1
Le circuit magnétique en acier de la figure comporte une bobine de 500 spires sur la branche médiane. Les dimensions sont : e=1\: mm (joint d'air); $S_1=300\hspace{0.17em}m{m}^2$; $S_2 =S_3=150\hspace{0.17em}m{m}^2$ ; $l_1=40\hspace{0.17em}mm$ ; $l_2=110\hspace{0.17em}mm$ ; $l_3=109\hspace{0.17em}mm$.
Trouver le courant nécessaire pour produire un flux de 0.125 mWb dans l'entrefer en supposant que $S_e$ (surface de l'entrefer) dépasse $S_3$ de 17 %.
La courbe de magnétisation de l'acier est donnée en annexe.
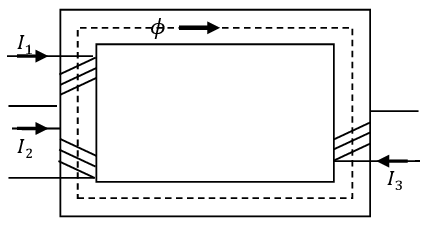
La perméabilité de l'air est : $\mu =4\hspace{0.17em}\Pi \hspace{0.17em}{10}^{-7}H{m}^{-1}$. Exercice 2
Le circuit magnétique en acier au silicium de la figure comporte deux bobines de 50 spires chacune et a partout la même section $S_1=1.3\hspace{0.17em}c{m}^2$ ; les longueurs moyennes sont $l_1=l_3=25\hspace{0.17em}cm$, $l_2=5\hspace{0.17em}cm$.
Trouver l’intensité des courants dans les bobines si ${\Phi }_1=0.09\hspace{0.17em}mWb$ et ${\Phi }_3=0.12\hspace{0.17em}mWb$.
Courbe de magnétisation de l’acier au silicium donnée (annexe).
Exercice 3
Un noyau magnétique dont la courbe magnétisante B(H) est la suivante, porte 3 bobines, conformément à la figure : $N_1=2000$ spires; $N_2=400$ spires; $N_3=1000$ spires ; $I_1=0.5A$; $I_2=1.0A$ ; $S=10c{m}^2$ ;$l=50 cm$.

B(T)	H(A/m)	B(T)	H(A/m)
0.3	52	1.25	380
0.4	58	1.3	600
0.5	65	1.35	900
0.6	76	1.4	1200
0.7	90	1.45	2000
0.8	110	1.5	3000
0.9	132	1.55	4500
1	165	1.6	6000
1.1	220	1.65	10000
1.2	300	1.7	14000

Quel courant $I_3$ doit-on envoyer dans la bobine 3 pour avoir un flux de 1.5 m Wb dans le noyau.
Exercice 4









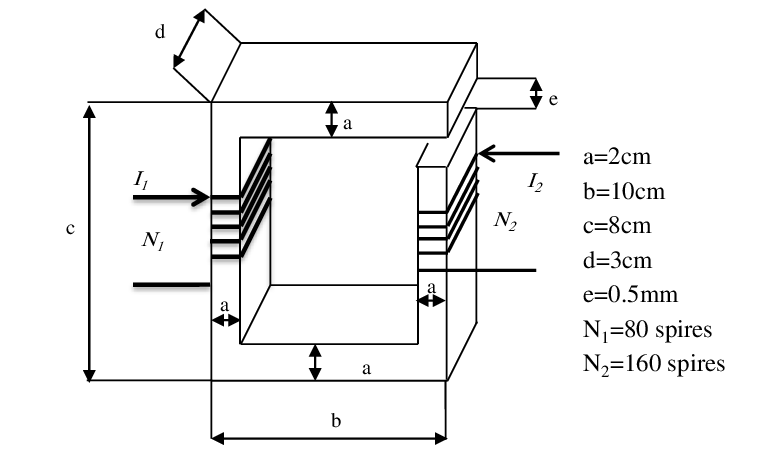
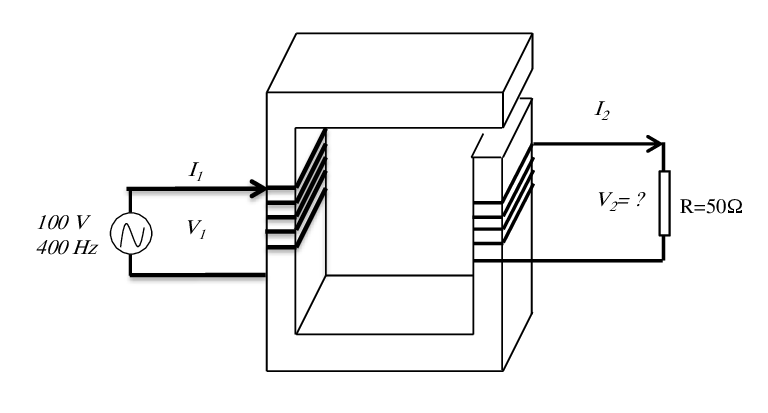
Soit le système électromagnétique de la figure. On suppose que la perméabilité du noyau magnétique est constante et égale à $2000{\mu }_0$. La résistance du fil de cuivre est négligeable.
Calculer l’inductance propre $L_1$de la bobine 1, l’inductance propre $L_2$ de la bobine 2, et l’inductance mutuelle M entre les deux bobines.
Une source de tension sinusoïdale 100 V (efficace) / 400 Hz est connectée à la bobine 1. Une résistance de $50\hspace{0.17em}\Omega$ est connectée à la bobine 2
Calculer la tension $V_2$ et le courant $I_1$. Exercice 5









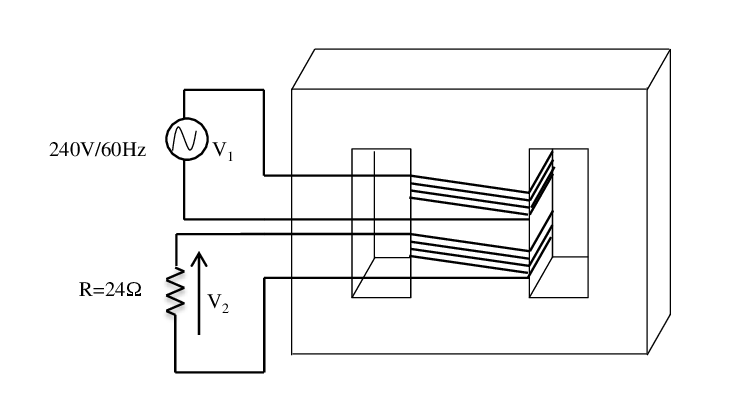
Soit le système électromagnétique de la figure. On suppose que la perméabilité du noyau magnétique est constante et égale à $3000{\mu }_0$. La résistance du fil de cuivre est négligeable.
Calculer l’inductance propre $L_1$de la bobine 1, l’inductance propre $L_2$ de la bobine 2, et l’inductance mutuelle M entre les deux bobines.
Une source de tension sinusoïdale 240V (efficace) / 60 Hz est connectée à la bobine 1. Une résistance de $24\hspace{0.17em}\Omega$ est connectée à la bobine 2
Calculer la tension $V_2$ et le courant $I_1$. Exercice 6
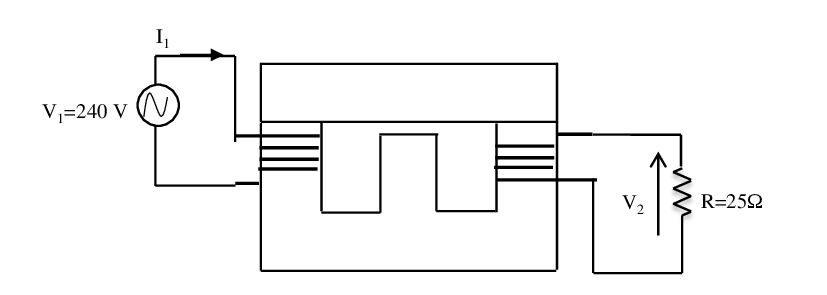
Soit le système électromagnétique de la figure
1. Tracer le circuit équivalent du système magnétique (sans calculer les valeurs des réluctances).











Pour déterminer les inductances propres et mutuelles, on réalise les deux montages de la figure suivante :










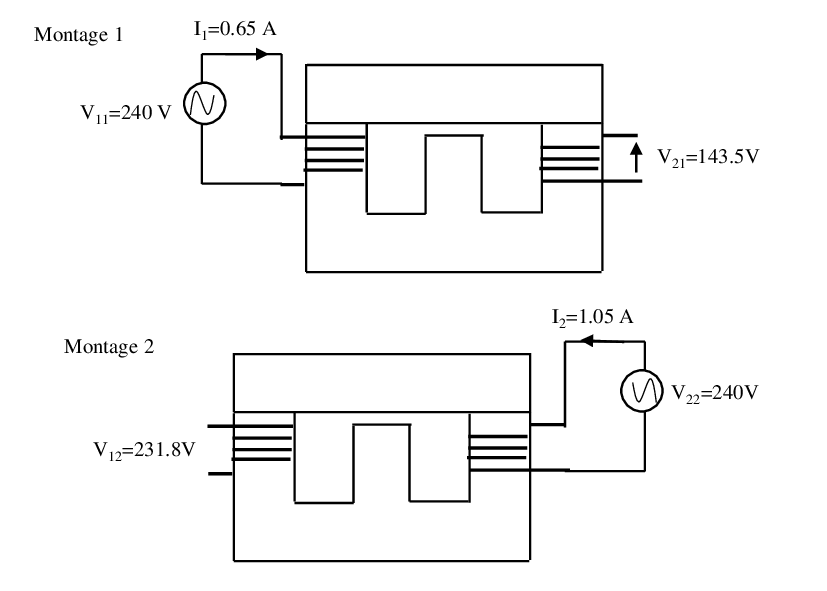
À partir des valeurs des tensions et courants obtenues dans ces deux montages, calculer les inductances propres $L_1$, $L_2$ et l’inductance mutuelle M$ des deux bobines.
Une source de tension sinusoïdale 240 V / 60 Hz est connectée à la bobine 1. Une résistance $R=25\Omega$ est connectée à la bobine 2. Calculer le courant $I_1$ (valeur efficace) dans la bobine 1 et la tension $V_2$ (valeur efficace) aux bornes de la résistance R.








Exercice 7
Soit deux bobines de 160 tours chaque sur le même noyau magnétique comme illustre la figure. On suppose que la perméabilité du noyau magnétique est constante et égale à $2500{\mu }_0$. On suppose aussi que la résistance du fil de cuivre est négligeable.
1. Calculer l’inductance propre de chaque bobine.
2. n fait circuler un courant continu de 1 A dans la bobine 1. La bobine 2 est en circuit ouvert. Calculer Le champ magnétique dans chacune des trois colonnes du noyau magnétique.
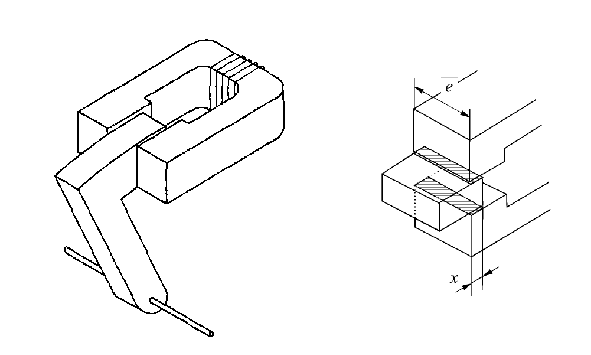
Exercice 8
Soit un électroaimant constitué d’un circuit magnétique déformable et d’une bobine de n spires comme illustré à la figure
Lorsqu’un courant circule dans la bobine un flux magnétique circule dans la pièce mobile provoquant une force susceptible de centrer la partie mobile dans l’entrefer afin de minimiser la réluctance du circuit magnétique.
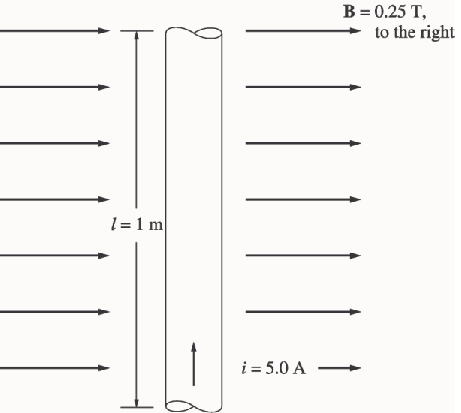
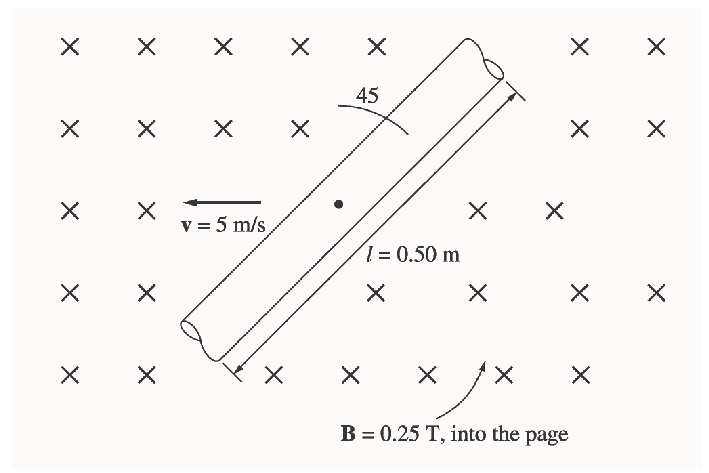
Exercice 9
Un conducteur est représenté sur la figure parcouru par un courant électrique de 5,0 A en présence d'un champ magnétique de 0.25 T.
Calculez l'intensité et la direction de la force induite sur le conducteur.



Exercice 10
Le conducteur représenté à la figure 3.55 se déplace en présence d'un champ magnétique. Avec les informations données sur la figure.\\\\
Déterminez l'amplitude et la direction de la tension induite dans le conducteur.



Exercice 11
Le noyau représenté magnétique présente le flux représenté à la figure.









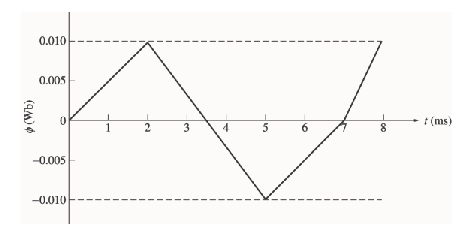
Tracer l'allure de la tension présente au bornes de la bobine.
Exercice 12
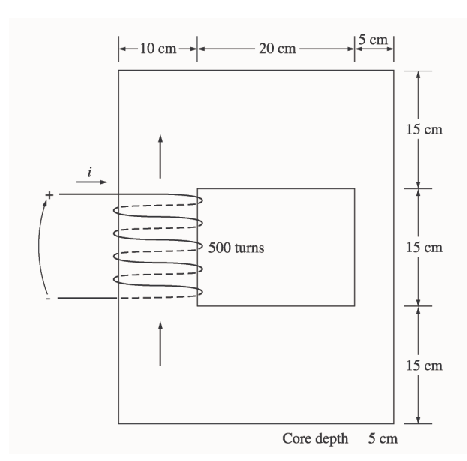
La figure représente le noyau d'un moteur à courant continu simples. dont on donne la courbe d’aimantation du métal dans ce noyau.









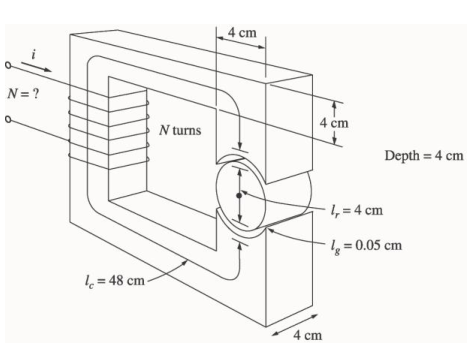
Supposons que le courant est de 1A et que la section de chaque entrefer est de 18 $c{m}^2$ et que sa largeur est de 0,05 cm. Le diamètre effectif du noyau du rotor est de 4 cm.









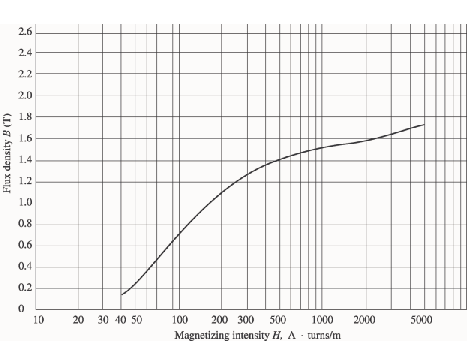
Calculer le nombre de spires N.
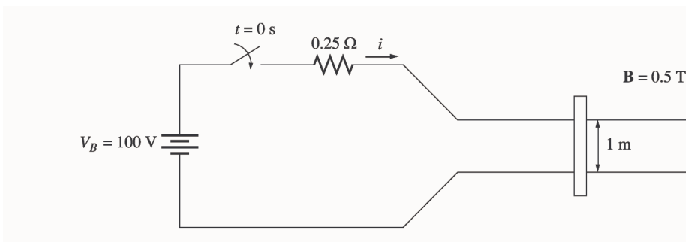
Exercice 13
Une machine linéaire a une densité de flux magnétique de 0,5 T dirigée vers la page, une résistance de $0,25\Omega$, une longueur de barre l = 1,0 m et une tension de batterie de 100 V.
1. Quelle est la force initiale sur la barre au démarrage? Quel est le courant initial?
2. Quelle est la vitesse à vide de la barre en régime établi?
3. Si la barre est chargée avec une force de 25 N opposée au sens du mouvement, quelle est la nouvelle vitesse constante? Quelle est l'efficacité de la machine dans ces circonstances?
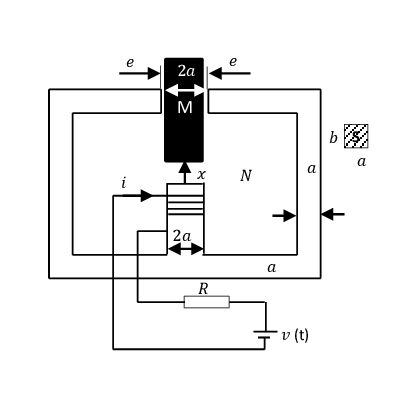
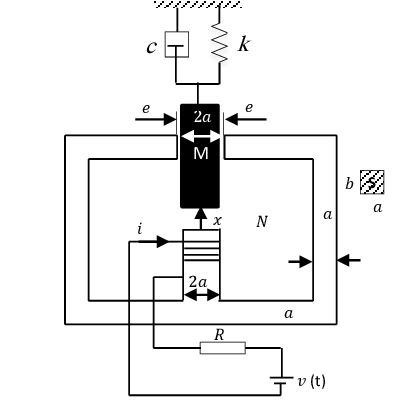
Exercice 14
Considérez le système électromécanique de la figure. Il consiste en une structure fixe en matériau magnétique hautement perméable ($\mu \to \infty$) avec un enroulement d'excitation de N spires.
Un piston mobile, également en matériau magnétique hautement perméable ($\mu ⟶\infty$), est contraint par un manchon non magnétique pour se déplacer dans la direction x.
Il s'agit de la configuration de base utilisée pour le déclenchement de disjoncteurs, de vannes de commande et d'autres applications dans lesquelles une force relativement importante est appliquée à un élément qui se déplace sur une distance relativement petite.
Nous souhaitons calculer l'inductance de la bobine (en fonction du courant i et du déplacement x) et de la tension v pour une variation temporelle spécifiée de i et x.
Exercice 15
Nous considérons à nouveau le système de champ magnétique illustré à la figure. l'inductance a été calculée dans l’exercice 14.
Nous incluons maintenant le type d’éléments électriques et mécaniques qui seront normalement présents lors de l’application de ce transducteur. La résistance R représente la résistance de l'enroulement plus toute résistance série supplémentaire dans le circuit externe.
Ce système est de la forme utilisée classiquement pour actionner des relais, des vannes, etc. par conséquent, la source v(t) est généralement positive ou négative.
Le ressort k est utilisé pour ouvrir l’écart x à sa largeur maximale lorsque le courant est nul.
L'amortisseur linéaire c représente le frottement entre le manchon non magnétique et le piston, bien que, dans certains cas, un amortissement supplémentaire soit ajouté de manière externe, soit pour ralentir le mouvement mécanique (comme dans un relais temporisé), soit pour réduire le rebond susceptible de se produire lorsque le piston atteint x = 0.
Calculer la force magnétique appliquée sur le piston.
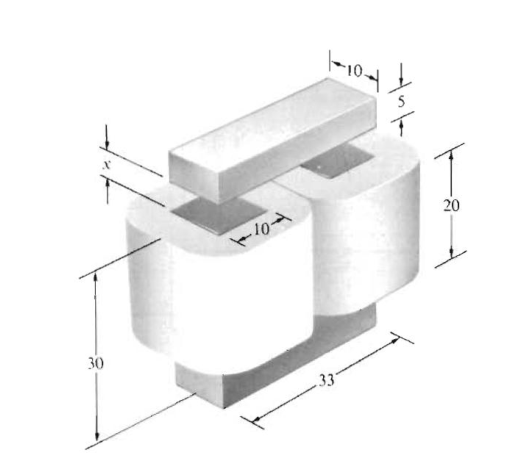
Exercice 16
La figure montre un petit électroaimant. Toutes les dimensions sont en millimètres. Chaque bobine a 500 spire et transporte un courant de 2 ampères.
1. Calcule B dans les entrefers en fonction de $x$. on donne $ \mu_r= 1000$. et on néglige le flux de fuite.
2. Calculer la force d’attraction exercée sur l’armature lorsque x =5 millimètres.
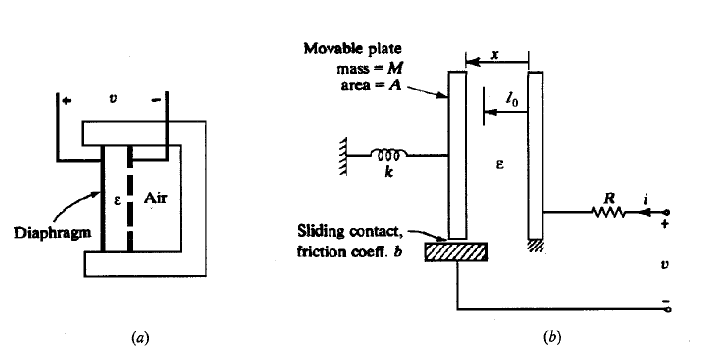
Exercice 17
Un microphone à condensateur illustré à la figure (a) peut être modélisé par le système électromécanique de la figure(b). Avec v comme entrée.
Obtenir les équations dynamiques du système.



Exercice 18
Les venteuses électromagnétique sont trés utilisé. Par exemple dans les cases automobiles : r = 5 cm, B = 1.5 T.
Calculer la force $F$.




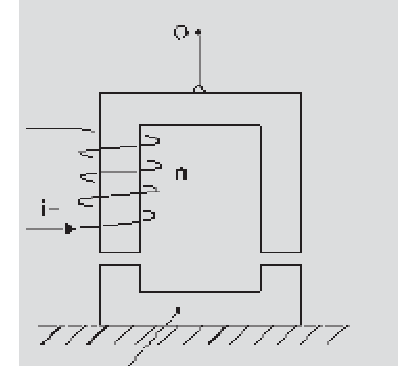Exercice 19
Un électroaimant est suspendu au point O à 2 mm au-dessus de son armateur posée sur le sol. Tous deux en fer doux (matériau magnétique hautement perméable : $\mu ⟶\infty$)de masse volumique 7800 $Kg/m^3$, de surface S=1.5 $c{m}^2$ par bras et de longueur moyenne L=42 cm pour l'électroaimant et l=14 cm pour l'amateur. On prendra $g=9.81m/s^2$.
Calculer l'induction à réaliser dans le circuit magnétique pour attirer l'armature.