Exercice 1









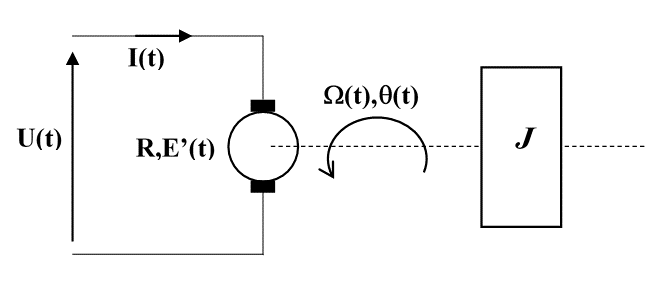
On considère le système décrit par la figure. L'inertie des parties tournantes (rotor, volant, etc...) est notée J et le coefficient de couple est notée K.
Pour modéliser le système, nous considérons les hypothèses suivantes :
- H1 : Le flux est créé par des aimants permanents, il est donc constant.
- H2 : La self de l'induit est négligée, seule sa résistance R est prise en compte.
- H3 : On néglige tous les couples résistants (frottements secs et visqueux).
1. Ecrire les équations différentielles régissant le fonctionnement du moteur puis leurs transformées de Laplace.
2. A partir de la question précédente, compléter le schéma bloc du moteur.








3. A partir du schéma bloc précédent et de la formule des systèmes bouclés, déterminer la fonction de transfert $T\left(s\right)=\frac{\Omega \left(s\right)}{U\left(s\right)}$
4. Déterminer le gain statique, puis le temps de réponse du système.
Exercice 2
La fonction de transfert du moteur est donnée par :
$H\left(S\right)=\frac{2.36}{a_2{S}^2+a_{1}S+1}, avec a_2=1.609\times {10}^{-6} et a_1=0.0056$
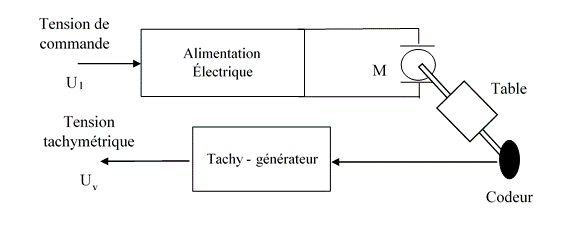
On équipe le moteur avec une dynamo tachymétrie qui mesure la vitesse. La caractéristique de ce capteur est un simple gain b exprimé en V/(rad/s). Puis on boucle selon le schéma suivant :







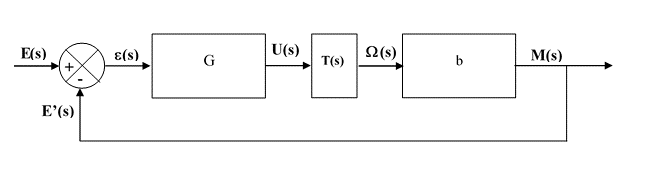
G est le gain réglable de l'amplificateur de puissance et M(t) est la mesure de la vitesse en volts. La mesure de vitesse est comparée à la consigne E. La fiche technique de la dynamo tachymétrie donne : 3 V pour 1000 t/mn.
1. Calculer la Fonction de Transfert en Boucle Fermée (FTBF)
2. En déduire les expressions du coefficient d'amortissement et de la pulsation propre en boucle fermée.
3. On veut régler l'amortissement de la boucle à 0.7, quelle valeur faut-il donner à G?
Exercice 3
Un asservissement de position angulaire d’un moteur à courant continu peut être représenté par le schéma-bloc de la figure. L'entrée est une tension (exprimée en volt) et la sortie est un angle (exprimée en radian).








On suppose que le correcteur est un simple amplificateur c.-à-d. C(p) = K.
1. Calculer la FTBF du système corrigé. En déduire les expressions du coefficient d’amortissement, de la pulsation propre et du gain statique G.
2. Justifier physiquement la valeur du gain statique.
3. On impose pour cette boucle un amortissement de 0.52 ; en déduire le réglage correspondant de K. Evaluer le temps de réponse.
4. La consigne est un échelon d'amplitude 2V c.-à-d. e(t) = 2u(t). Calculer la sortie S1 en régime permanent (S est une position angulaire qui s'exprime en radian).
5. On considère maintenant un correcteur PI, Déterminer la fonction de transfert en boucle fermée du système.
6. En utilisant le critère de Routh, determiner pour quelles valeurs de K et Ti le système reste stable en boucle fermé.
7. A partir du résultat de la question précédente, expliquer pourquoi la technique de réglage par compensation (c-a-d T1 = 0.1s) , n'est pas pertinante ici.
8. On utilise un correcteur PID non standard dont la fonction de transfert est donnée par :
$C\left(s\right)=K\frac{\left(T_1 s+1\right)\left(T_2 s+1\right)}{T_1 s}$
On choisit de compenser la constante de temps du système à corriger en _xant T1 = 0:1s.
8.1. Determiner la fonction de transfert en boucle fermée du système.
8.2. En utilisant le critère de Routh, montrer que le système en boucle fermé reste stable quelque soit la valeur de K et T1. Ce résultat est-il surprenant ?
8.3. Determiner les expressions de l'amortissement m1 et de la pulsation propre du système en boucle fermée. Pour répondre à cette question, on negligera la présence du zéro au numérateur.
8.4. On impose un amortissement m = 0.52 et un temps de réponse tr = 0.5s. En déduire les valeurs de K et T2.

Exercice 4











Pour le moteur on donne la fonction de transfert $H\left(s\right)=\frac{2}{1+0.04s}$
1. Donner le schéma bloc du système
2. Calculer la fonction de transfert en boucle ouverte du système.
3. On veut réaliser un asservissement en position avec un correcteur du type P .
3.1. Donner le schéma bloc du système
3.2. Déterminer la fonction de transfert en boucle ouverte.
3.3. Déterminer la fonction de transfert en boucle fermée.
3.4. Calculer Kp pour que le temps de réponse à 5% après une excitation échelon de position soit le plus faible possible.
3.5. Calculer le temps de réponse.

Exercice 5
On donne : $\frac{U_V\left(s\right)}{U_1\left(s\right)}=\frac{1.2}{1+0.25s}$











1. On veut réaliser un asservissement en position avec un correcteur du type P G(p)=Kp.
1.1. Donner le schéma bloc du système
1.2. Déterminer la fonction de transfert en boucle fermée.
1.3. Calculer Kp pour que le temps de réponse à 5% après une excitation échelon de position soit le plus faible possible. Calculer le temps de réponse.

Exercice 6
On boucle un moteur à courant continu représenté F(s) selon le schéma de la figure. Le système F(s) possède un gain statique K, un amortissement $\zeta$ et une pulsation propre ωn.








1. Ecrire F(s) sous la forme canonique.
2. Calculer la fonction de transfert en boucle fermée G(s) (calcul littéral).
3. Déterminer, pour G(s), la valeur de la pulsation propre.
4. En déduire l'expression de l'amortissement pour G(s) en fonction de K, A et $\zeta$.
5. On donne K = 2, $\zeta$= 1.5 et ωn = 50 rad/s-1. Calculer la valeur numérique de A permettant d'obtenir en boucle fermée un amortissement de 0,5.

Exercice 7
Soit un moteur CC P=3.7KW ; R=11.4 Ω ; L=0.1214 H ; J=0.02215 Kg m^2; Bm=0.002953 Nms/rad ; Kb=0.0045 Vs/rad ; Kt=1.28 Nm/A
1. Modéliser le système sachant que $E=K_b\Omega$ et $T_{em}=K_T I$
2. En utilisant la transformée de Laplace, déterminer que la fonction de transfert /V est de la forme :
$\frac{\Omega \left(s\right)}{V\left(s\right)}=\frac{K_T}{\left[LJ\right]s^2+\left[RJ+L{B}_m\right]s+\left[R{B}_m+K_b{K}_T\right]}$, Application numérique
3. Ecrire la fonction de transfert sous la forme canonique et Déduire les valeurs de facteur d’amortissement, le gain statique et la pulsation propre
4. On veut réaliser un contrôle de vitesse, le régulateur utilisé est un régulateur PID. Représenter le schéma de commande.
5. En utilisant la compensation des pôles, déterminer les paramètres du régulateur PID en fonction du facteur d’amortissement.
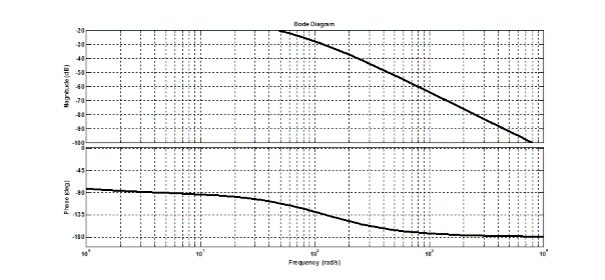
6. On donne la réponse fréquentielle de la fonction de transfert, déterminer par la méthode de N-Z les paramètres du régulateur PID.






















Exercice 8
L'asservissement de la position d'un moteur à courant continu est représenté par le schéma-bloc de la figure







Où B = 20 et $\tau$ = 0:1s. On étudiera diverses solutions pour améliorer certaines performances du système. On cherche dans un premier temps à obtenir un amortissement $\zeta$ = 0,5.
Le paramètre à étudier est l'écart de traînage évalué lorsque l'entrée est une rampe avec une pente unitaire. Réglage de l'amortissement.
1. Calculer le gain A1 nécessaire pour obtenir un amortissement de 0,5.
2. A partir de la valeur A1, déterminer la valeur de l'écart de trainage.
3. Déterminer la valeur du temps de réponse, tr.
Correction tachymétrique.
On modifie la structure de l'asservissement en introduisant une boucle supplémentaire dite de correction tachymétrique







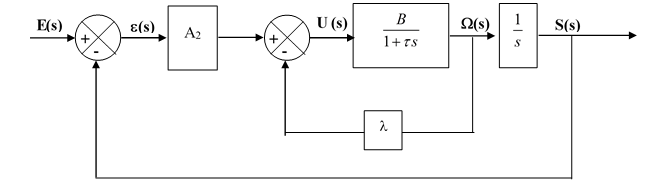
1. Montrer que la boucle interne (entre U(s) et Ω(s)) est équivalente à : $H\left(s\right)=\frac{B_0}{1+{\tau }_{0}s}$ dont on précisera les expressions de B0 et ${\tau }_0$. On est donc ramené au cas précédent
2. On cherche à obtenir un écart de traînage Δ2 = Δ1/10 tout en stabilisant la boucle avec un coefficient d'amortissement $\zeta$= 1 (on ne tolère aucun dépassement). En déduire les valeurs qu'il faut régler pour les gains A2 et $\lambda$.
3. Déterminer la nouvelle valeur du temps de réponse tr.