Exercice 1
Système 1
- Cahier de charge : un temps de réponse de 30 ms
- Déterminer les paramètres du correcteurs PI.








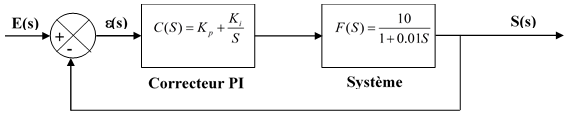
Système 2
- Cahier de charge : un temps de réponse de 30 ms et un facteur d’amortissement de 0.7
- Déterminer les paramètres du correcteurs PI.








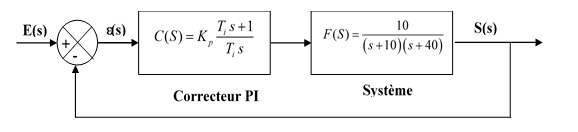
Exercice 2
Un entrainement électromécanique du 1er ordre est asservi selon la boucle classique







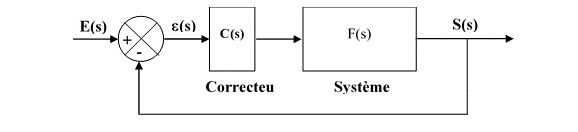
La fonction de transfert du système a été déterminée à partir de mesures en boucle ouverte :
$F\left(S\right)=\frac{2}{1+0.1S}$
1. Le correcteur C(p) étant pour l'instant indéterminé, calculer l'expression de la Fonction de Transfert en Boucle Fermée (FTBF).
On impose à cette FTBF d'être identique à un modèle du 2ème ordre Hm(s) caractérisé par les paramètres suivants : - Un facteur d’amortissement de 0.8.
- tr : 1/5e du temps de réponse du système non corrigé en boucle ouverte,
- Gain statique égal à 1 (pas d'erreur statique).
2. Déterminer la fonction de transfert Hm(s).
3. Calculer alors l'expression du correcteur C(s).
Exercice 3
Soit un entrainement électromécanique dont on donne la fonction de transfert
$F\left(S\right)=\frac{2}{1+0.1S}$
On considère un correcteur PI standard $C\left(S\right)=K_p\frac{T_i s+1}{T_i s}$
On va étudier par les techniques de Correction par compensation des pôles pour le réglage des paramètres Ti et Kp.
1. Donner l'expression de FTBO lorsque Ti = 0.1s.
2. A partir du résultat précédant, calculer la FTBF du système ainsi corrigé.
3. Déterminer la valeur de Kp permettant d'obtenir un temps de réponse égal à 1/5e du temps de réponse du système non corrigé en boucle ouverte.
Exercice 4
Soit un entrainement électromécanique dont on donne la fonction de transfert $F\left(S\right)=\frac{2}{1+0.1S}$
On considère un correcteur PI standard $C\left(S\right)=K_p\frac{T_i s+1}{T_i s}$
On souhaite conserver un correcteur type PI standard et on cherche à régler K et Ti.
1. Calculer l'expression littérale de la FTBF.
2. Calculer à présent K et Ti permettant d'imposer à la FTBF les mêmes pôles que ceux du modèle Hm(s) du 2e ordre établi à l’exercice 2 (i.e. le dénominateur de la FTBF doit être identique à celui du modèle précédent).

Exercice 5
Soit $F\left(S\right)=\frac{1}{{\left(1+S\right)}^3}$; la fonction de transfert d’un système asservi à l’aide d’un régulateur PID.
la réponse fréquentielle est donnée par la figure





















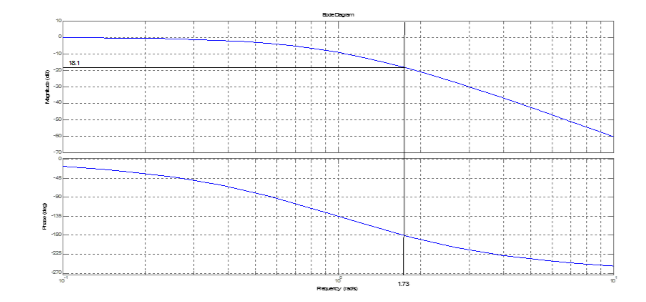
1. Déterminer par la méthode de Ziegler-Nichols les 3 paramètres du régulateur
Exercice 6
Soit $F\left(S\right)=\frac{1}{{\left(1+S\right)}^3}$ ; la fonction de transfert d’un système asservi à l’aide d’un régulateur PID.
la réponse indicielle, est donnée par la figure





















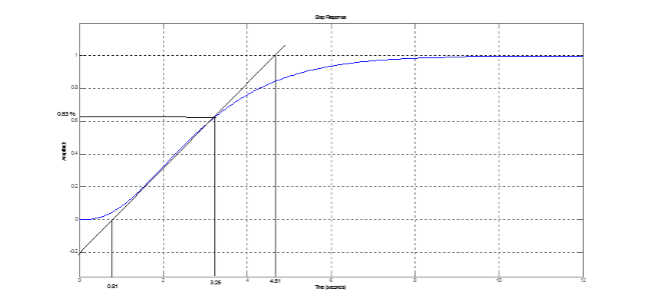
1. Déterminer par la méthode de Ziegler-Nichols les 3 paramètres du régulateur