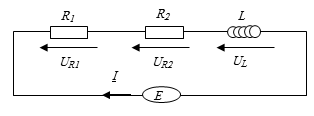
Exercice 1
Pour le circuit série de la Figure, on donne :
$E\left(t\right)=282 sin \omega t$; $R_1=6 \Omega$; $R_2=4 \Omega$; $L=0.0191 H$; $\omega =314rad/sec$.
Déterminer le courant et la tension aux bornes des éléments du circuit.



Exercice 2
Une puissance de 300 W est dissipée dans le circuit série suivant dont le facteur de puissance est de 0.6 (inductif).
Déterminer la puissance apparente absorbée ainsi que l’impédance série Z(R,X) du circuit .

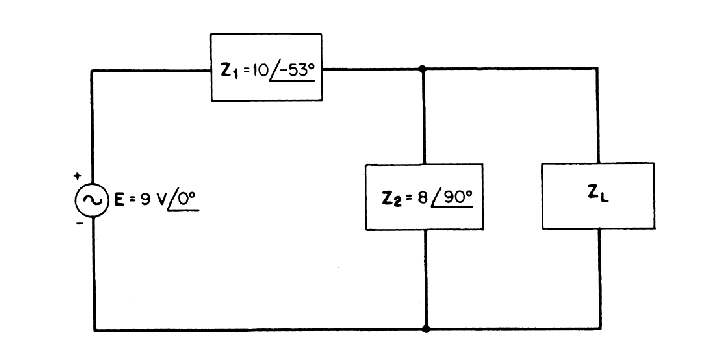
Exercice 3
Soit le récepteur d’impédance $Z(R,X)$ alimenté sous U=220 V, 50Hz, 100A, le déphasage de U sur I est de 53° inductif. Ce récepteur est relié à un générateur de fem E par une ligne d’impédance $Z_L=0.15+j0.25$.
1. Calculer les éléments R et X du récepteur Z (supposés en série).
2. Calculer la fem $\overline{E}$.

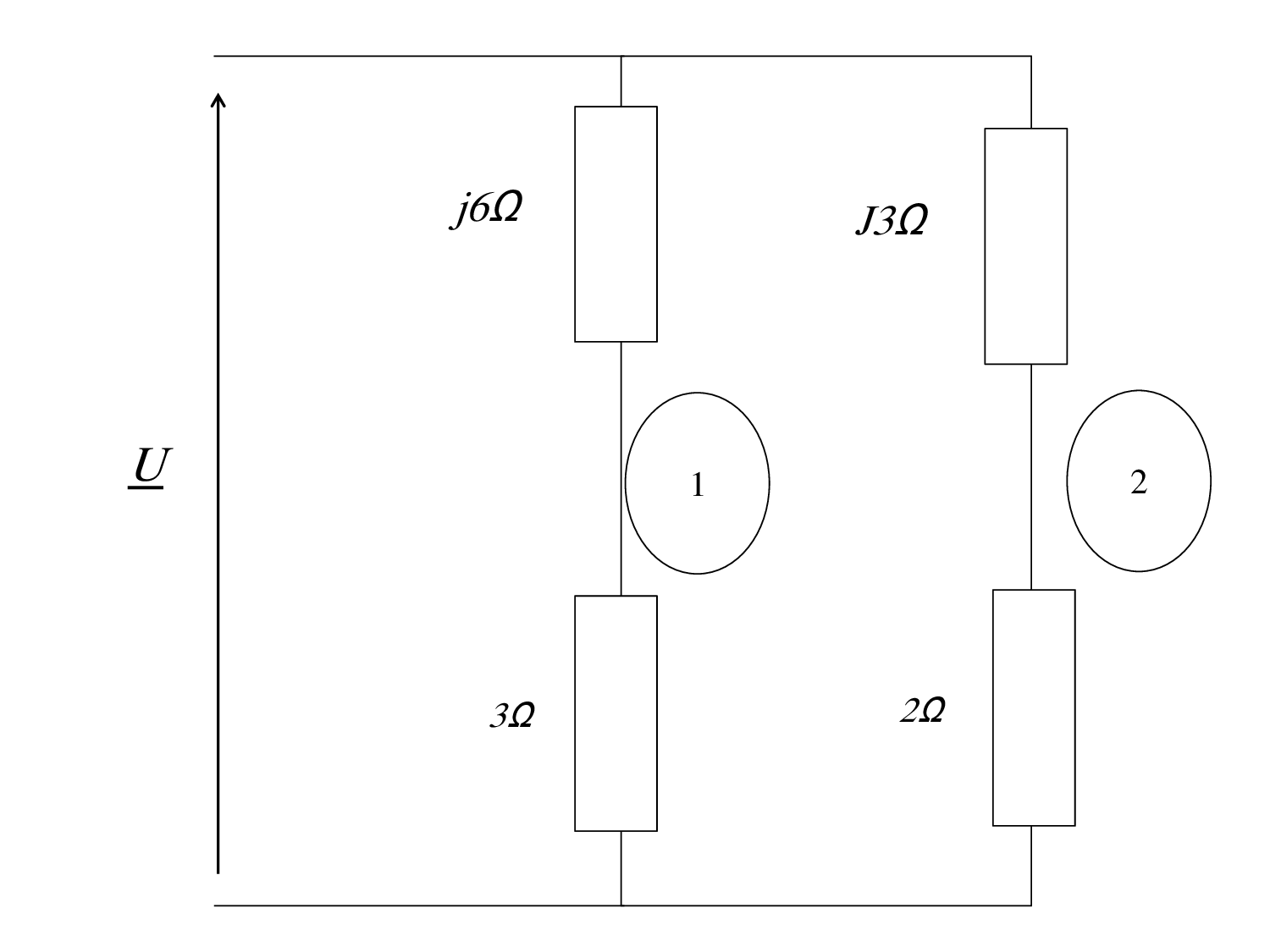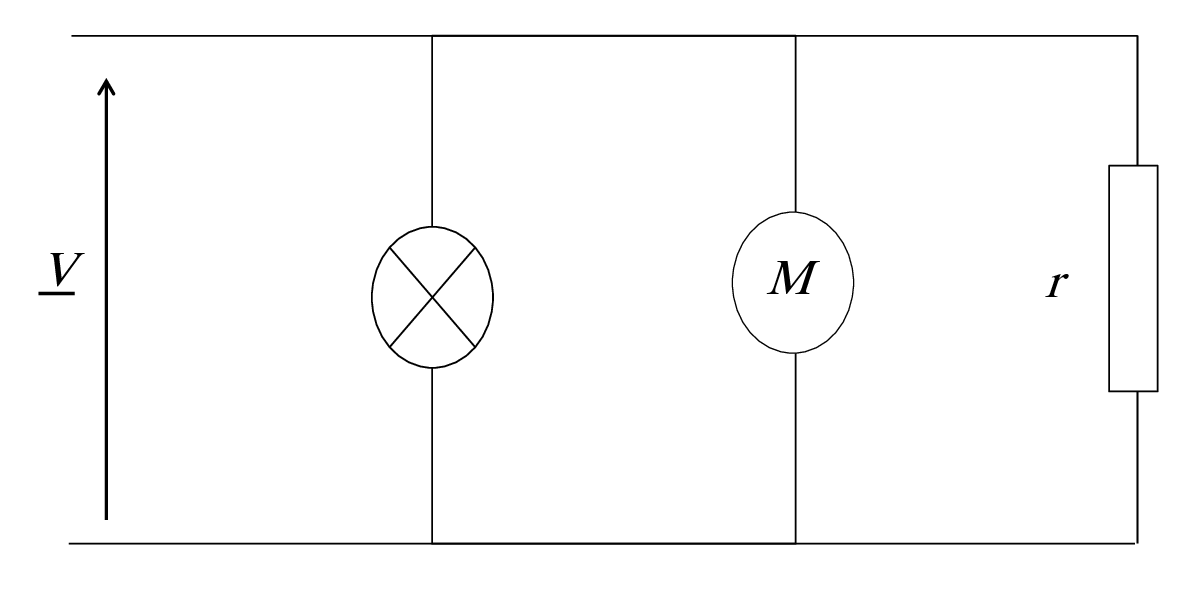
Exercice 4
La branche 1 du circuit de la figure 4 absorbe une puissance de 1490 VAR.
Calculer la puissance active consommée par tout le circuit et le courant total.


Exercice 5
Une entreprise comporte trois ateliers, dont les puissances respectives consommées sont :$S_1=25\hspace{0.17em}kVA ; \cos \hspace{0.17em}{\phi }_1=0.6 \left(inductif\right); S_2=40\hspace{0.17em}kVA; \cos \hspace{0.17em}{\phi }_2=0.8 \left(inductif\right); S_3=60\hspace{0.17em}kVA; \cos \hspace{0.17em}{\phi }_3=0.9 \left(capacitif\right)$.
1. Déterminer la puissance apparente totale consommée par l’entreprise.
2. Déterminer le facteur de puissance total de l’entreprise.
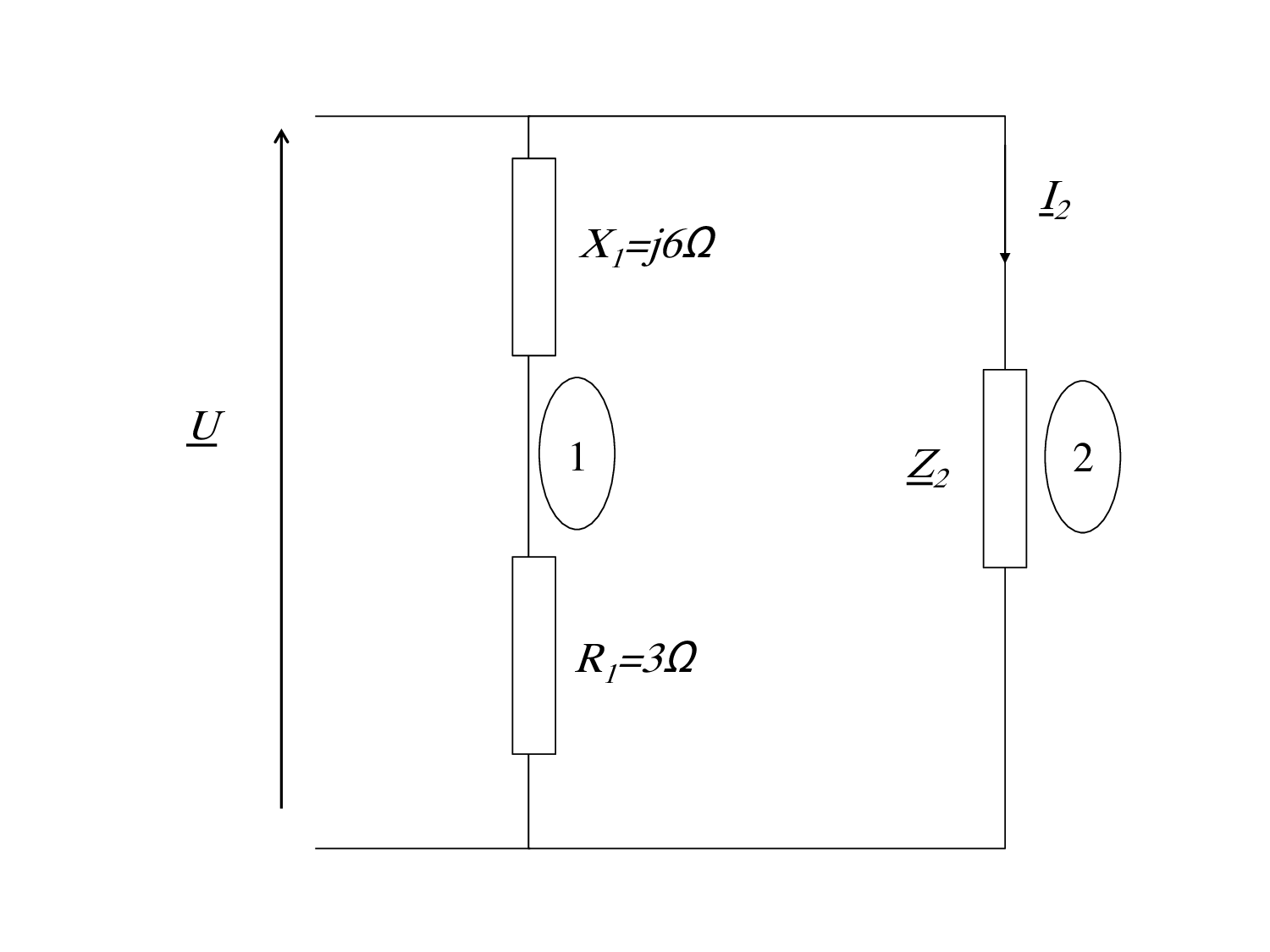Exercice 6
Dans le circuit suivant, dont le facteur de puissance est de 0.937 (capacitif), la résistance $R_1=3\hspace{0.17em}\Omega$ dissipe une puissance de 666 W et la puissance apparente totale pour tout le circuit est de 3370 VA
1. Calculer l’impédance série Z(R,X).

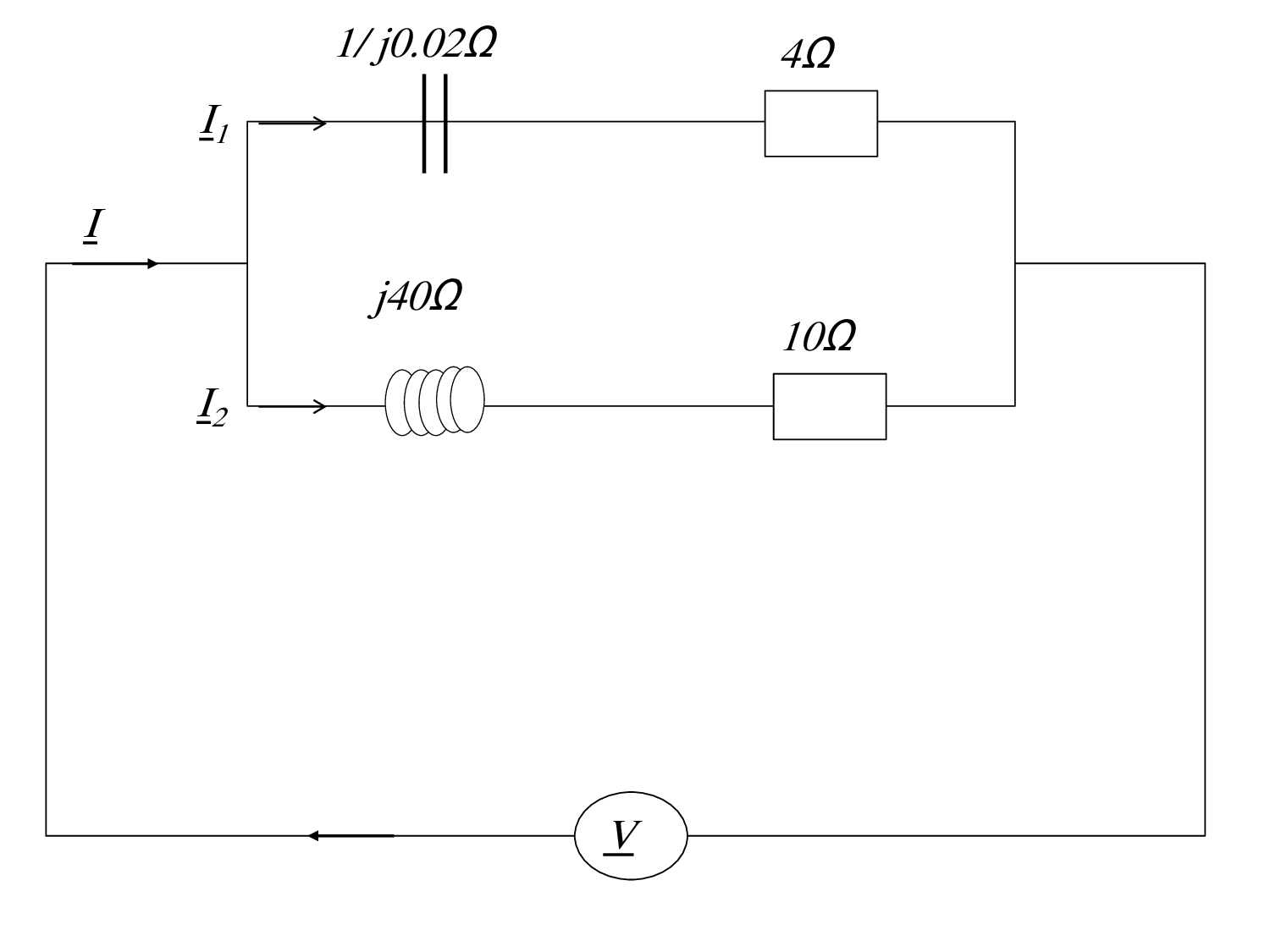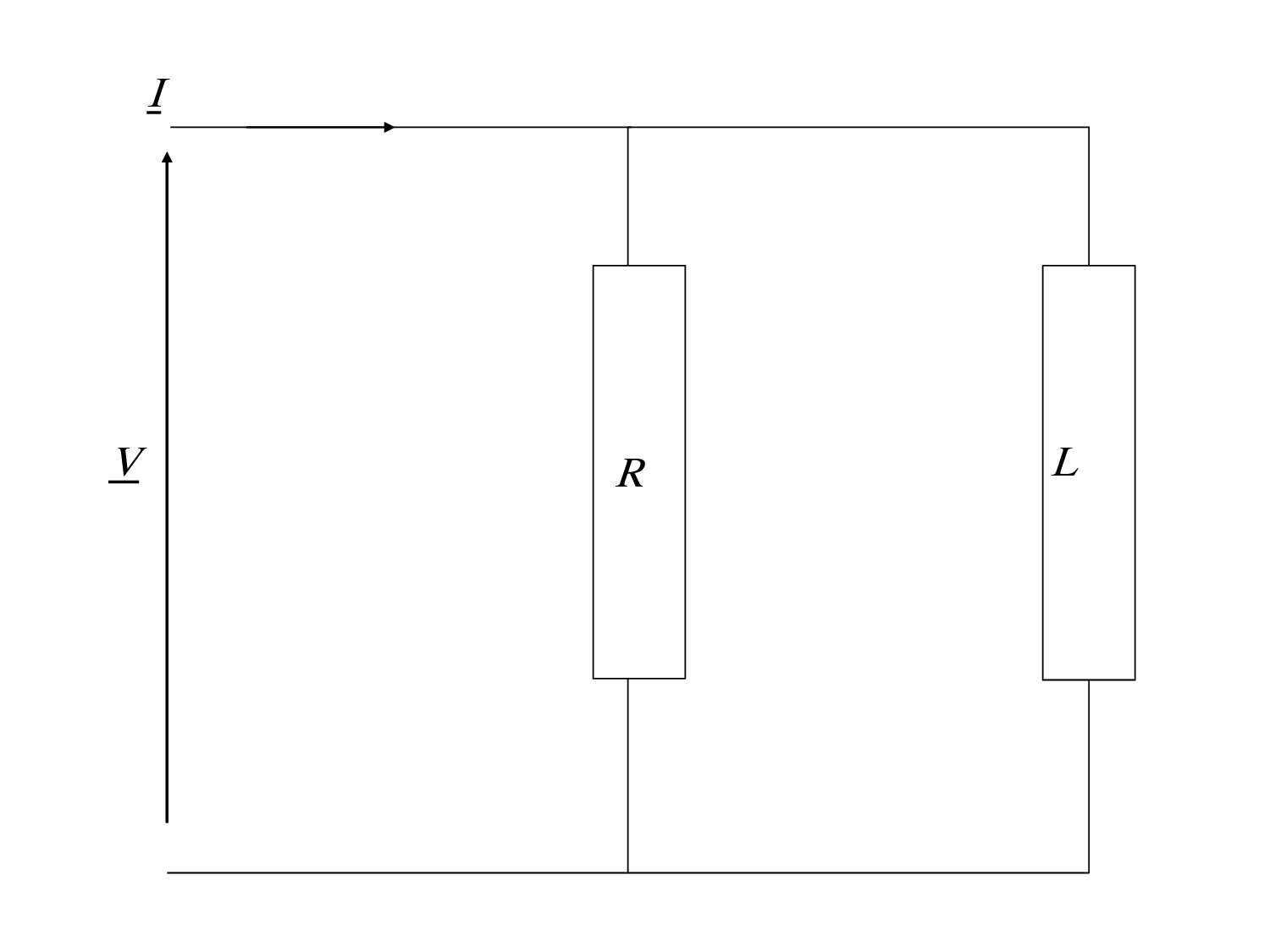
Exercice 7
Dans circuit représenté sur la figure, on ne connaît que la valeur du courant total absorbé I=2.5\:A ainsi que les valeurs des impédances notées sur la figure.
1. Calculer la valeur de la tension efficace V appliquée à cette charge.
2. En déduire les valeurs efficaces de $I_1$ et $I_2$.

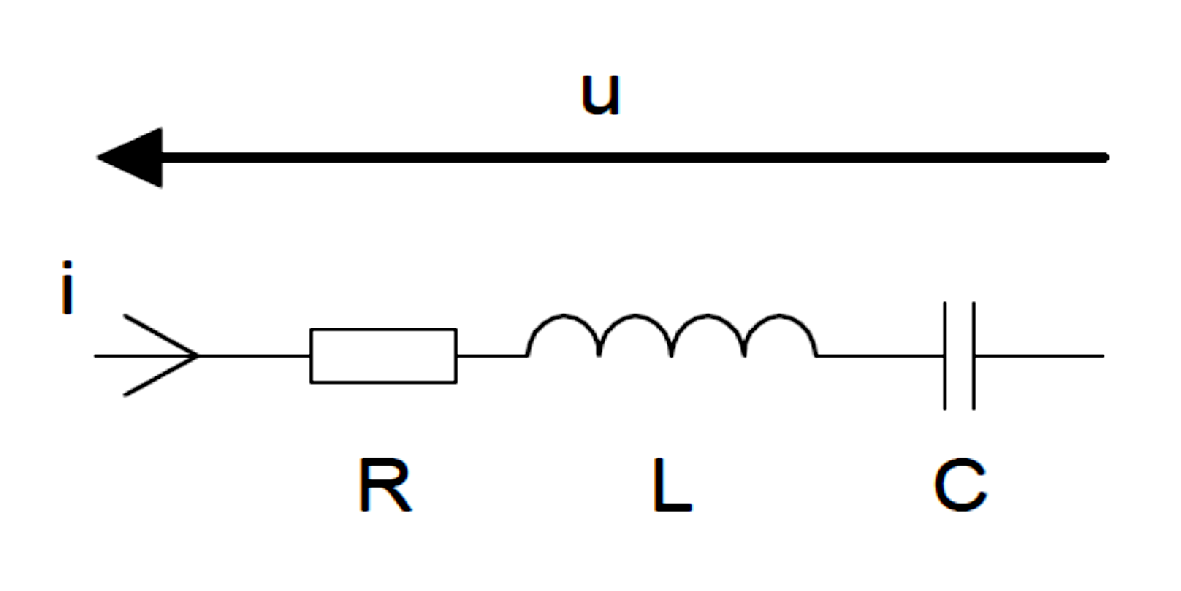
Exercice 8
On donne V = 230 V, f = 50 Hz, R = 1.6 k $\Omega$ et L = 1.25 H.
1. Calculer la puissance active P consommée par la charge.
2. Calculer la puissance réactive Q consommée par la charge.
3. Calculer la puissance apparente S du circuit.
4. En déduire I (en valeur efficace) et le facteur de puissance du circuit.

Exercice 9
1. Déterminer l’impédance complexe $\overline{Z}$ du circuit.
2. Exprimer P, Q et S en fonction de I.
3. A la résonance u et i sont en phase. Que vaut alors Q
4. En déduire la fréquence de résonance.

Exercice 10
Une installation électrique monophasée 230 V / 50 Hz comporte :
- une ampoule de 75 W chacune ;
- un radiateur électrique de 1.875 kW ;
- un moteur électrique absorbant une puissance de 1.5 kW avec un facteur de puissance de 0.80.
Ces différents appareils fonctionnent simultanément.
1. Quelles sont les puissances active et réactive consommées par l’installation ?
2. Quel est son facteur de puissance ?
3. Quelle est l’intensité efficace du courant dans le câble de ligne ?
Exercice 11 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Calculer l'impédance de charge de la figure. 1.37 pour une puissance maximale de la charge $Z_L$.









Exercice 12 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Quelle est la capacité C qui doit être fournie par le condensateur de la Figure pour améliorer le facteur de puissance à 0,95.









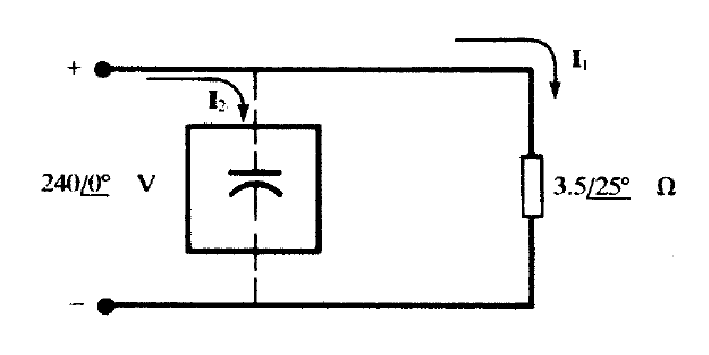
Exercice 13 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
La Figure illustre un système d'alimentation monophasé en courant alternatif simple avec trois charges. La source de tension est $\underline{V}=120\hspace{0.17em}\angle 0^o\hspace{0.17em}V$ et les trois charges sont ${\underline{Z}}_1=5\hspace{0.17em}\angle \hspace{0.17em}{30}^o\hspace{0.17em}\Omega$, ${\underline{Z}}_2=5\hspace{0.17em}\angle \hspace{0.17em}{45}^o\hspace{0.17em}\Omega$, ${\underline{Z}}_3=5\hspace{0.17em}\angle \hspace{0.17em}-{90}^o\hspace{0.17em}\Omega$.








Répondre aux questions suivantes sur ce système d'alimentation.
1. Supposons que l'interrupteur illustré sur la figure soit ouvert et calculons le courant $\underbar{I}$, le facteur de puissance, et la puissance réelle (active), réactive et apparente fournie par la source.
2. Supposons que l'interrupteur illustré sur la figure soit fermé et calculons le courant $\underbar{I}$, le facteur de puissance, et la puissance réelle, réactive et apparente fournie par la source.
3. Qu'est-il arrivé au courant $I$ lorsque l'interrupteur s'est fermé? Pourquoi?

Exercice 14 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Le chauffage par induction électromagnétique correspond à beaucoup d’applications industrielles et par exemple, pour les bijoutiers, à la fusion de métal comme l’argent.
Une bobine inductrice placée à l’extérieur d’un creuset, qui renferme l’argent à liquéfier, crée de forts courants induits dans l’argent. L’effet joule créé par ces courants chauffe le métal jusqu’à son point de fusion.
Schéma de principe.








Le four à induction, dans les conditions nominales de fonctionnement, est modélisé électriquement par une inductance pure (L) placée en série avec une résistance (r).








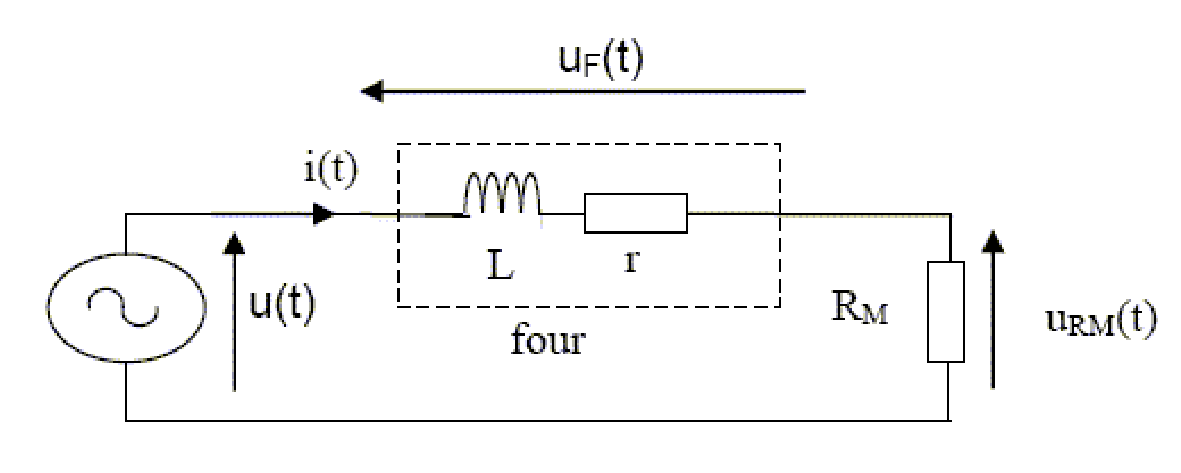
L’objectif de cette partie est de déterminer de deux manières différentes les caractéristiques électriques (L,r) d’un four à induction de bijoutier.
On place en série avec le four à induction une résistance de mesure $RM$ comme indiqué sur la figure
Avec : 1. u(t) : tension d’alimentation sinusoïdale alternative
2. i(t) : courant d’alimentation sinusoïdal alternatif
3. $u_F\left(t\right)$ : tension aux bornes du four à induction
4. $u_{RM}\left(t\right)$ : tension aux bornes de la résistance de mesure
5. $RM=10,0\hspace{0.17em}m\Omega$ (résistance de mesure).








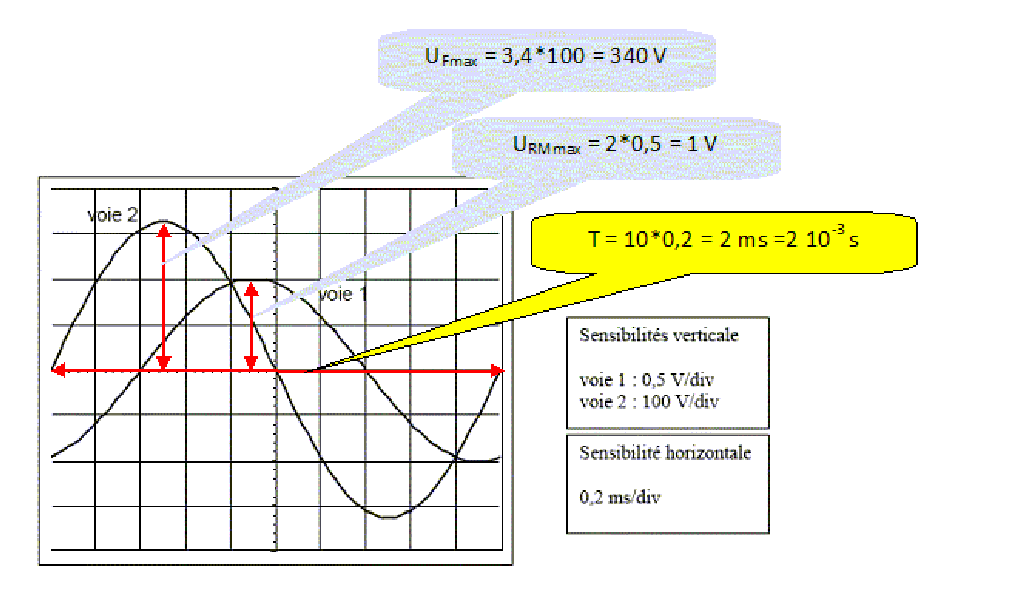
Un oscilloscope permet de visualiser simultanément la tension $u_{RM}\left(t\right)$ sur la voie 1 et la tension $u_F\left(t\right)$ sur la voie 2.
On observe alors les oscillogrammes de la figure.
1. Déterminer la période et la pulsation de la tension $u_F\left(t\right)$.
2. Déterminer les valeurs maximales $U_{RMmax}$ et $U_{Fmax}$ des tensions $u_{RM}\left(t\right)$ et $u_F\left(t\right)$.
Pour la suite du problème, on prendra $U_F=230\hspace{0.17em}V$ et ${\phi }_{UF/i}=1,26rad$. Le four à induction se modélise donc comme indiqué sur la figure.









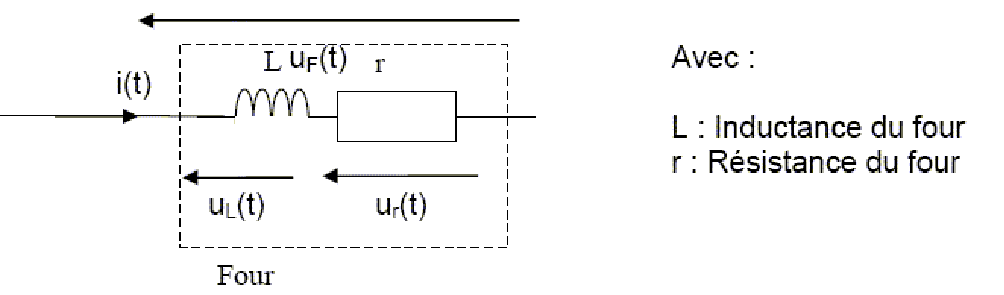
1. Tracer le vecteur de Fresnel $U_F$ associé à la tension $u_F\left(t\right)$ avec $i\left(t\right)$ comme référence des phases. (échelle : 1 cm correspond à 20 V )
2. Rappeler la valeur du déphasage ${\phi }_{UL/i}$ de la tension $u_L\left(t\right)$ par rapport au courant i(t) pour le cas de l’inductance pure L.
3. De même rappeler la valeur du déphasage ${\phi }_{Ur/i}$ de la tension $u_r\left(t\right)$ par rapport au courant i(t) pour le cas d’une résistance r.
4. En déduire le seul tracé possible pour les vecteurs $U_L$ et $U_r$ associés aux tensions $u_L\left(t\right)$ et $u_r\left(t\right)$. Effectuer le tracé des vecteurs sur le graphe précédent.
5. Déduire, graphiquement, que la valeur efficace $U_r$ de la tension $u_r\left(t\right)$ est de 70 V et que la valeur efficace $U_L$ de la tension $u_L\left(t\right)$ est de 220 V.
Un wattmètre mesure la puissance active consommée par le four : P = 5.00 kW.
Une mesure directe du courant appelé par le four donne I = 70,9 A.
La tension aux bornes du four a pour valeur efficace UF = 230 V et pour une fréquence f= 500 \: Hz.
Le four à induction est toujours modélisé par une inductance pure $L$ en série avec une résistance r.
1. Quelle est la puissance active $P_L$ consommée par l’inductance pure L ?
2. En déduire la puissance active $P_r$ consommée par de résistance r.
3. Calculer la valeur de la résistance r.
4. Calculer le facteur de puissance du four.
5. Calculer la valeur de l’inductance L du dipôle r,L série qui modélise le four.
6. Quelle est la valeur de la capacité à ajouter en série pour augmenter le facteur de puissance à 0,9
7. Pour quoi en cherche à augmenter le facteur de puissance ?
Exercice 15 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une ligne de transmission monophasée ayant une résistance de $R_L=10\Omega$ est connectée à une tension émettrice fixe de $E_s=1000\hspace{0.17em}V$.
Calculer :
1. La puissance maximale que la ligne peut transmettre à la charge
2. En utilisant la figure calculer la tension correspondante du récepteur 3. La puissance du récepteur pour une tension de récepteur de $E_R=950\hspace{0.17em}V$
La puissance maximale pour une ligne résistive est donnée par: $P_{max}=\frac{E_s^2}{4\hspace{0.17em}{R}_L}$.













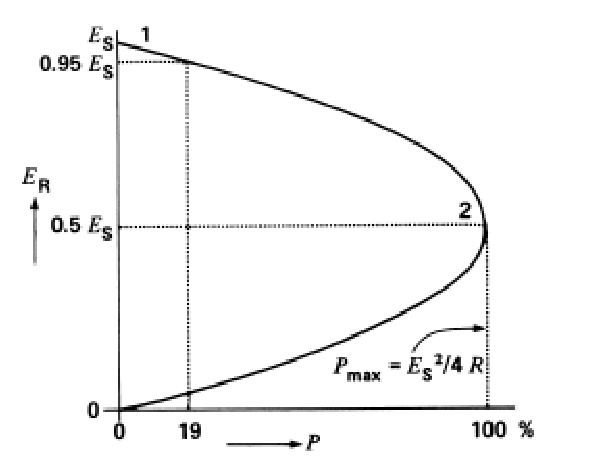
Exercice 16 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une ligne de transmission monophasée ayant une inductance de $X_L=10 \Omega$ est connectée à une tension émettrice fixe de $E_s=1000\hspace{0.17em}V$.
Calculer :
1. La puissance maximale que la ligne peut transmettre à une charge résistive
2. En utilisant la figure calculer la tension correspondante du récepteur
3. La puissance du récepteur pour une tension de récepteur de $E_R=950\hspace{0.17em}V$














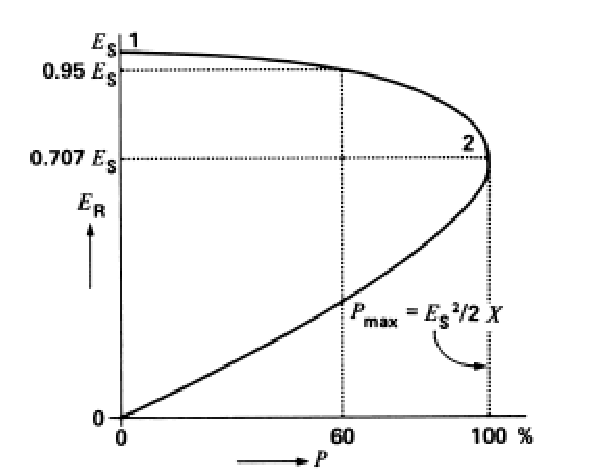
Exercice 17 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une ligne monophasée possède une réactance inductive $X_L=10\hspace{0.17em}\Omega$ et est connectée à une tension émettrice fixe de $E_s=1000\hspace{0.17em}V$.
S'il est totalement compensé ($Q_c=0.5Q_L$), calculer ce qui suit:
1. La puissance active maximale que la ligne peut fournir à une charge résistive.
2. La réactance capacitive $X_C$ à installer.
La puissance maximale est donnée par:$P_{max}=\frac{E_s^2}{X_L}$














Exercice 18 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un réacteur ayant une réactance inductive de $4\hspace{0.17em}\Omega$ est connecté aux bornes d'un générateur de 120 V alternative (Figure).
1. Calculer la valeur du courant dans le réacteur
2. Calculer la puissance associée au réacteur
3. Calculer la puissance associée au générateur de courant alternatif.
4. Tracer le diagramme de phase du circuit















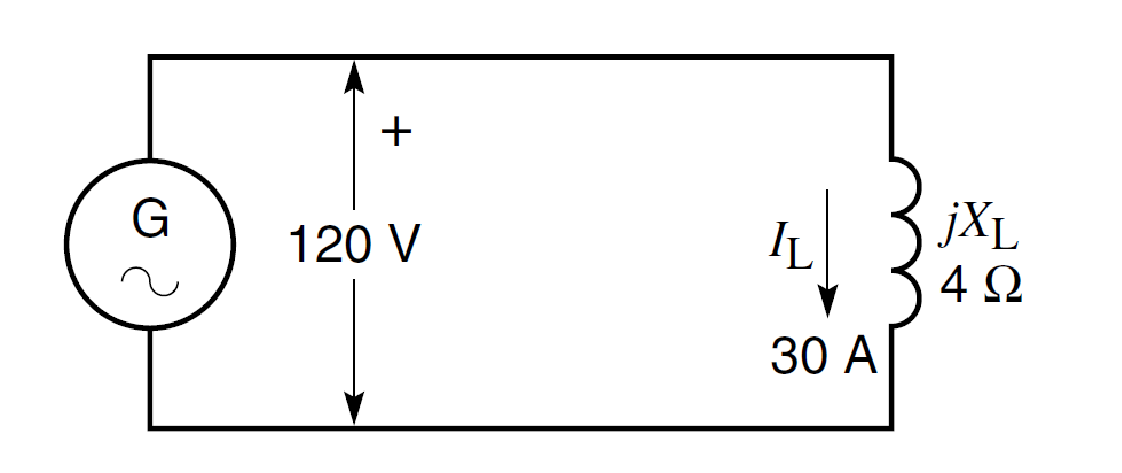
Exercice 19 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un générateur de courant alternatif G est connecté à un groupe d’éléments de circuit R, L, C (figure 1.48). Les éléments respectifs portent les courants indiqués.
Calculer la puissance active et réactive associée au générateur.















Exercice 20 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur à courant alternatif absorbe 40 kW de puissance active et 30 kvar de puissance réactive.
1. Calculer la puissance apparente fournie au moteur.
2. Calculer le facteur de puissance du moteur

Exercice 21 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur monophasé absorbe un courant de 5 A d'une ligne 120 V, 60 Hz. Le facteur de puissance du moteur est de 65 %.
Calculer
1. La puissance active absorbée par le moteur
2. La puissance réactive fournie par la ligne
Un condensateur de $50 \mu F$ est placé à travers le moteur. Calculer
3. La puissance réactive générée par le condensateur
4. La puissance réactive absorbée par la ligne
5. Le nouveau courant de ligne

Exercice 22 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Sur la figure, la tension entre les bornes 1 et 3 est 60 V.








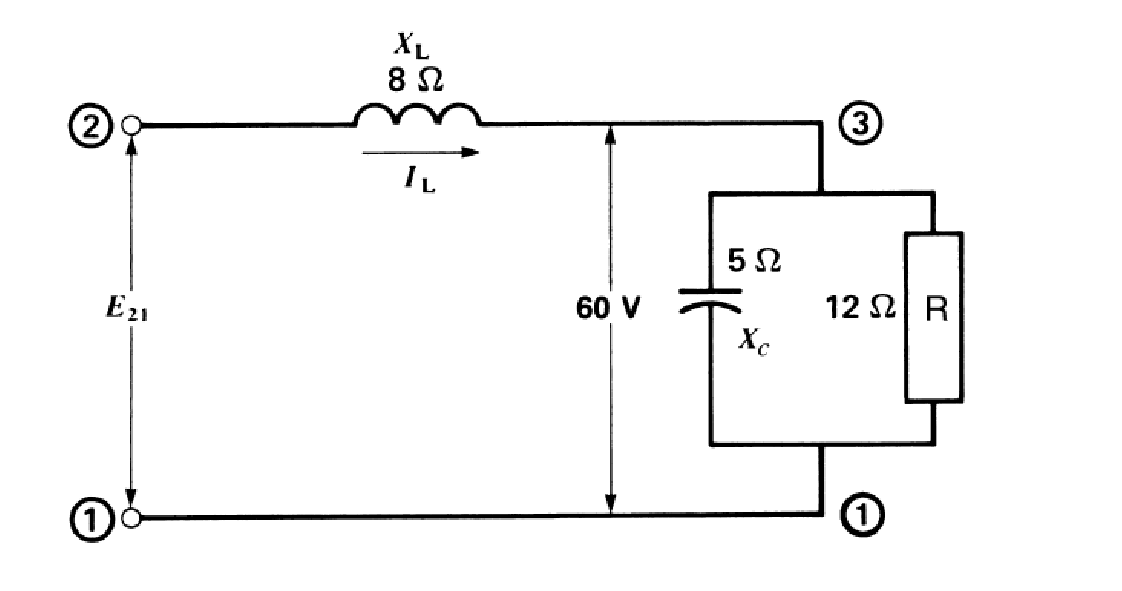
1. Le courant dans chaque élément de circuit.
2. La tension entre les bornes 1 et 2
3. L'impédance entre les bornes 1 et 2
Exercice 23 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une ligne de transport monophasée de 12,47 kV, longue de plusieurs kilomètres, alimente une charge C provenant d'une sous-station (Figure).








La ligne a une résistance de $2,4 \Omega$ et une réactance de $15 \Omega$.
Les instruments de la sous-station indiquent que les entrées d'alimentation active et réactive de la ligne sont de 3 MW et 2 Mvar, respectivement.
Calculer
1. Le courant de ligne et son angle de phase par rapport à la tension de ligne de la sous-station
2. La puissance active absorbée par la charge
3. La puissance réactive absorbée par la charge
4. La tension de ligne à la charge
5. L'angle de phase entre la tension à la charge et celle à la sous-station

Exercice 24 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Le circuit de la Figure est composé d’une résistance $45\hspace{0.17em}\Omega$ connecté en série avec une réactance inductive à $28\hspace{0.17em}\Omega$.








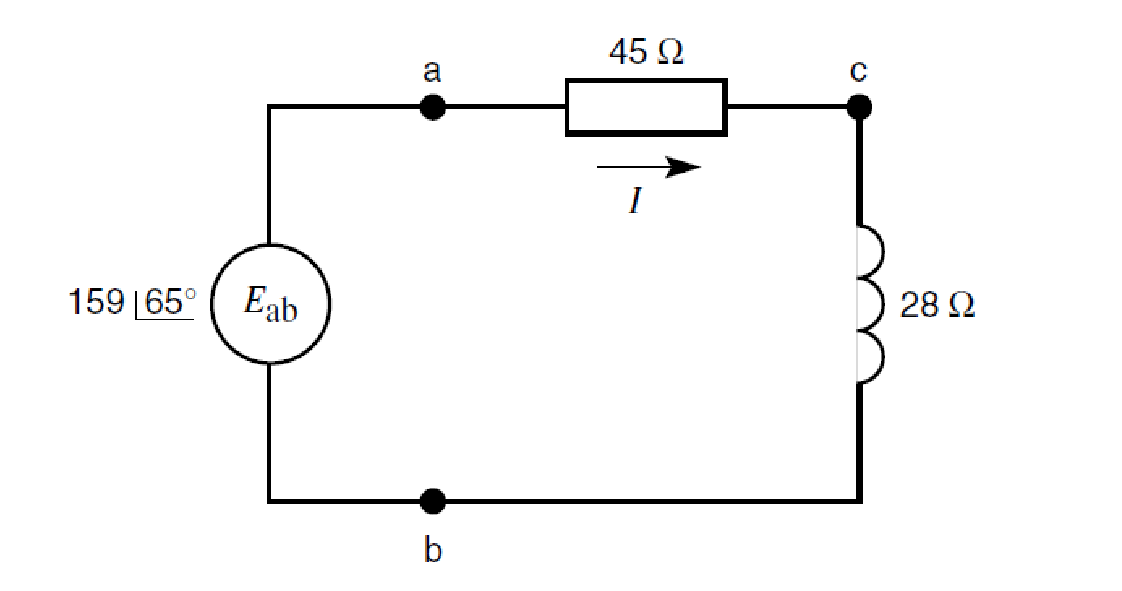
La source génère une tension décrite par le phaseur $E_{ab}=159\hspace{0.17em}\angle \hspace{0.17em}65$.
Calculer :
1. Le module et la phase du courant I
2. Le module et la phase de la tension aux bornes de la résistance et de la réactance
3. La puissance active et réactive associée à la résistance, à la réactance et à la source.

Exercice 25 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un gros moteur absorbe 600 kW avec un facteur de puissance de 90 %.
Calculer la puissance apparente et la puissance réactive absorbées par la machine.

Exercice 26 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un condensateur de 200 $\mu F$ est connecté à une source 240 V, 60 Hz.
Calculer la puissance réactive générée.

Exercice 27 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une résistance de 10 $\Omega$ est connectée sur 120 V, Source 60 Hz.
Calculer
1. La puissance active absorbée par la résistance
2. La puissance apparente absorbée par la résistance

Exercice 28 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur monophasé consomme un courant de 12 A avec un facteur de puissance de 60 %.
Calculer les composantes en phase et en quadrature du courant $I_p$ et $I_q$ par rapport à la tension de ligne.

Exercice 29 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur monophasé tire un courant de 16 A d'une ligne 240 V, 60 Hz. Un wattmètre connecté à la ligne donne une lecture de 2765 W.
1. Calculer le facteur de puissance du moteur et la puissance réactive absorbée.
Si un condensateur ayant une réactance de 30 $\Omega$ est connecté en parallèle avec le moteur, calculer
2. la puissance active indiquée par wattmètre
3. La puissance réactive totale absorbée par le condensateur et le moteur
4. La puissance apparente absorbée par la ligne
5. Le courant de ligne
6. Le facteur de puissance de la combinaison moteur - condensateur

Exercice 30 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur à induction absorbe une puissance apparente de 400 kVA avec un facteur de puissance de 80 %.
Calculer
1. La puissance active absorbée par le moteur
2. La puissance réactive absorbée par le moteur
3. A quoi sert la puissance réactive

Exercice 31 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur ayant un facteur de puissance de 0,8 absorbe une puissance active de 1200W.
Calculer la puissance réactive tirée de la ligne.

Exercice 32 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Une ligne monophasée de 13,2 kV, 60 Hz relie un poste électrique à une charge industrielle. La ligne a une résistance de 2,4 $\Omega$ et une réactance de 12 $\Omega$.
L'équipement de comptage de la sous-station indique que la tension de la ligne est de 12,5 kV et que la ligne consomme 3 MW de puissance active et 2 MVAR de puissance réactive.
Calculer
1. Le courant circulant dans la ligne
2. La puissance active et réactive consommée par la ligne
3. La puissance active, réactive et apparente absorbée par la charge
4. La tension à travers la charge

Exercice 33 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un moteur monophasé de 2 ch, 230 V, 1 725 tr / min, 60 Hz, fabriqué par Baldor Electric Company, présente les caractéristiques suivantes:
- Courant à pleine charge: 11,6 A - rendement: 75,5 % - facteur de puissance: 74 %
Calculer
1. La puissance active et réactive absorbée par cette machine lorsqu'elle fonctionne à pleine charge.
2. Si un condensateur de 40 $\mu \hspace{0.17em}F$ est connecté aux bornes du moteur, calculer le courant de ligne alimentant le moteur.
3. La présence du condensateur affectera-t-elle la température du moteur?

Exercice 34 (Ajouté le 8 novembre 2019 - أضيف بوم8-11-2019)
Un appareil de chauffage monophasé absorbe 4 kW sur une ligne de 240 V. Un condensateur connecté en parallèle à la résistance fournit 3 kVAR à la ligne.
1. Calculer la valeur du courant de ligne.
2. Si le condensateur est retiré, calculer le nouveau courant de ligne.